Асимптота

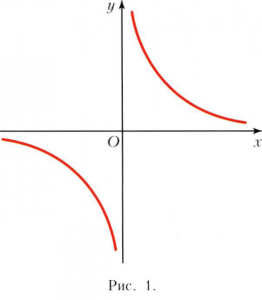
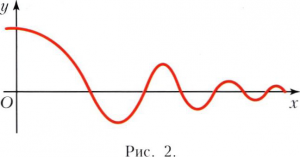
АСИМПТОТА (от греческого ασ?μπτωτος - несовпадающий, не касающийся) кривой с бесконечной ветвью, прямая, к которой эта ветвь неограниченно приближается; например, для гиперболы у=1/х (рис. 1) асимптотами являются оси координат Ох и Оу. Кривая может пересекать свою асимптоту (например, график затухающих колебаний на рисунке 2).

Кривые с бесконечными ветвями могут не иметь асимптоты (например, у параболы нет асимптоты). Если график функции у = f(x) при X →∞ имеет асимптоту, определяемую уравнением у = ах + b, то эта функция может быть пред­ставлена в виде f(x) = ах + b + α(х), где α(х) → 0 при х→∞.

Термин «асимптота» (применительно к гиперболе) приписывают Аполлонию Пергскому.