Базис

БАЗИС в математике, минимальный набор элементов, через которые можно выразить (представить) все элементы рассматриваемого множества или пространства. Понятие базиса используется в алгебре, функциональном анализе, геометрии, топологии, математической логике. В зависимости от раздела математики, где используется понятие базиса, слова «минимальный», «выразить» («представить») приобретают конкретное содержание. Важнейшим примером базиса в конечномерном действительном (комплексном) векторном пространстве R"(С"), состоящем из векторов с координатами х₁, ..., x_n, является набор векторов {е₁ ..., e_n}, где e_k - вектор, каждая координата которого равна 1, а остальные равны нулю, k=1, ..., n. Любой элемент пространства R"(С") можно выразить как линейную комбинацию элементов {е₁,...,e_n }, то есть как сумму этих элементов, умноженных на числа. Минимальность здесь означает, что никакая часть набора {е₁, ..., e_n } этим свойством не обладает.

Векторные пространства, в которых нет конечного базиса, называют бесконечномерными. В бесконечномерных сепарабельных банаховых пространствах базис определяют как счётный набор элементов {е₁, е₂, ...}, обладающий следующим свойством: любой элемент х пространства представим единственным образом в виде ряда

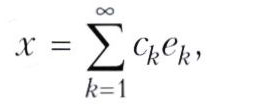
где c_k, k= 1,2,..., — числа, а ряд сходится по норме пространства. Известная проблема Банаха о существовании базиса в произвольном сепарабельном банаховом пространстве была отрицательно решена шведским математиком П. Энфло (1974). В банаховых пространствах можно определить базисы разных типов, их изучение - предмет содержательной теории. В сепарабельных гильбертовых пространствах наибольшее применение находят ортонормированные базисы, то есть такие базисы e₁,e₂, ..., для которых ска­лярные произведения (е_i,е_j) = 0, i≠j, и (е_i,е_i) = 1, i = 1, 2, ... . Важнейшим при­мером базиса в пространствах L_p[0, 1], р> 1, состоящих из функций, интегрируемых в р-й степени по Лебегу, является триго­нометрическая система {e^2πinx}^∞_{n= -∞}. Эта сис­тема - ортонормированный базис в L₂[0,1 ], а в L₁[0,1] она базисом не является.

А. А. Шкаликов.