Бесселя функции

БЕССЕЛЯ ФУНКЦИИ, цилиндрические функции 1-го рода; используются при изучении физических процессов (теплопроводности, диффузии, колебаний и пр.), рассматриваемых в областях с круговой и цилиндрической симметрией. Бесселя функции являются решениями Бесселя уравнения.

Бесселя функции J_p порядка (индекса) р, -∞<р<∞, представляется сходящимся при всех Х рядом

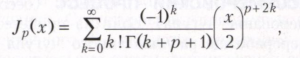
где Г - гамма-функция. График J_p(х) при х > 0 представляет собой кривую с затухающими колебаниями; J_p(х) имеет бесконечное множество нулей; первые слагаемые ряда дают асимптотику J_p(х) при малых |х|, при больших х>0 справедливо асимптотическое представление

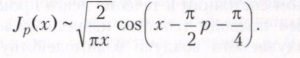
Бесселя функции порядка р = n + 1/2, где n - целое число, выражаются через элементарные функции; в частности,

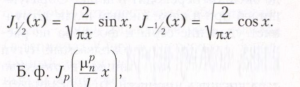
µ_n^p - положительные корни уравнения J_p(х) = 0, р > - 1/2, l - некоторое положительное число, образуют ортогональную с весом х систему на интервале (0, l).

Функция J₀ была впервые исследована Д. Бернулли в работе, посвящённой колебаниям тяжёлых цепей (1732). Л. Эйлер, рассматривая задачу о колебаниях круглой мембраны (1738), пришёл к уравнению Бесселя с целыми значениями р = n и нашёл выражение J_n(х) в виде ряда по степеням х, позднее он распространил это выражение на случай произвольных значений р. Ф. Бессель в связи с изучением движения планет вокруг Солнца исследовал (1824) функции J_p(х) и составил первые таблицы для J₀(х), J₁(х).

Лит.: Ватсон Г. Н. Теория бесселевых функций. М., 1949. Ч. 1-2; Лебедев Н. Н. Специальные функции и их приложения. 2-е изд. М.; Л., 1963; Бейтмен Г., Эрдейи А. Высшие трансцендентные функции. Функции Бесселя, функции параболического цилиндра, ортогональные многочлены. М., 1974.