Бейеса формула
Смотрите также:
БЕЙЕСА ФОРМУЛА, одна из основных формул элементарной теории вероятностей. Пусть A1, ..., An - некоторые несовместные (несовместимые) события, объединение которых - достоверное событие, и В - некоторое событие, Р(A1), ..., Р(An), Р(В) > 0 - их вероятности. Тогда условная вероятность события Ak при условии, что наступило событие В, может быть определена по формуле,
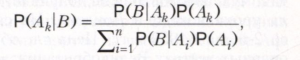
где k=1, ..., n, Р(В|Ai) - условная вероятность события В при условии, что наступило событие Ai.
Бейеса формула доказана Т. Бейесом (опубликовано в 1763 году), она является следствием теоремы умножения вероятностей. В применениях Бейеса формулы события Ak называют обычно гипотезами, вероятности Р(Ak) - априорными вероятностями, а вероятности Р(Ак|В) - апостериорными вероятностями этих гипотез. Непосредственное использование Бейеса формулы в качестве основы для статистических выводов из результатов наблюдений затрудняется тем, что, как правило, отсутствуют достаточно обоснованные данные об априорных вероятностях гипотез. По этой причине отношение к Бейеса формуле неоднократно пересматривалось. Бейеса формула используется в рамках так называемого бейесовского подхода к решению статистических задач.
Лит.: Бернштейн С. Н. Теория вероятностей. М., 1946; Боровков А. А. Математическая статистика. М., 1984.
Ю. В. Прохоров.