Биения

БИЕНИЯ, периодические изменения амплитуды (интенсивности) колебаний, возникающие при наложении двух или большего числа гармонических колебаний с близкими частотами. Пусть, например, имеются два колебания с амплитудами A₁, А₂, угловыми частотами ω₁, ω₂ и фазами φ₁ φ₂:

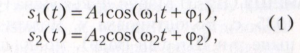
где t - время, а разность частот Δω = = ω₂ - ω₁ отлична от нуля. Выразив частоту второго колебания как ω₂ = ω₁+Δω, можно суммарное колебание s(t) = s₁+s₂ записать в виде:

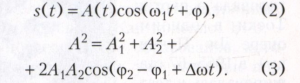
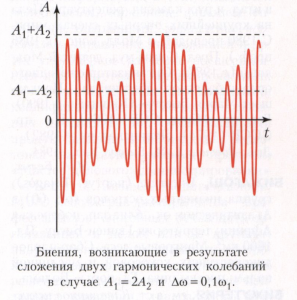
При Δω << ω₁) и Δω << ω₂ выражение (2) можно рассматривать как модулированное по амплитуде колебание с несущей частотой coj, причём мгновенная амплитуда А(t) периодически изменяется от A₁ +А₂ (рисунок) в моменты, когда cos(φ₂-φ₁) = 1, до |A₁-А₂|, когда cos(φ₂-φ₁) = -1. При A_l=А₂ в последнем случае происходит полное взаимное гашение двух колебаний. Частота изменений амплитуды (частота биения) Δω оказывается тем ниже, чем ближе частоты слагаемых колебаний ω₁ и ω₂, и при ω₁—> ω₂ исчезает («нулевые» биения).

По частоте биения можно с большой точностью определять разность частот двух колебаний и измерять различные параметры, влияющие на частоту реальных генераторов колебаний (ёмкости, индуктивности и др.), что широко используется на практике, например, при настройке музыкальных  инструментов (в этом случае биения воспринимаются на слух). Возникновение относительно низкочастотных биений при сложении колебаний применяется в радиотехнике при гетеродинном приёме высокочастотных сигналов (смотри Гетеродин). Нерегулярные биения могут возникать и при одинаковых частотах колебаний из-за неизбежного случайного дрейфа их фаз; это позволяет контролировать стабильность фазы генераторов путём наложения сигналов генератора и высокостабильного эталонного источника.

Лит.: Горелик Г. С. Колебания и волны. 2-е изд. М., 1959; Пейн Г. Физика колебаний и волн. М., 1979.