Броуновское движение

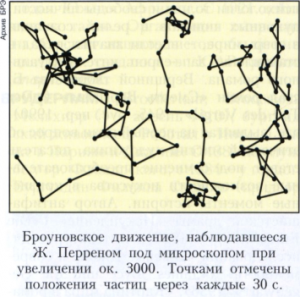БРОУНОВСКОЕ ДВИЖЕНИЕ (брауновское движение), беспорядочное движение малых (размером в несколько мкм и менее) частиц, взвешенных в жидкости или газе. Названо по имени Р. Броуна, открывшего явление в 1827 году. Видимые только под микроскопом взвешенные частицы движутся независимо друг от друга и описывают сложные зигзагообразные траектории (рис.). Броуновское движение не ослабевает со временем и не зависит от химических свойств среды. Интенсивность Броуновского движения увеличивается с ростом температуры среды и уменьшением её вязкости и размеров частиц.

Движение частиц происходит вследствие их соударений с окружающими молекулами. Объяснение Броуновскому движению было дано А. Эйнштейном и М. Смолуховским в 1905-06 годах на основе молекулярно-кинетической теории (смотри Кинетическая теория газов). Общая картина Броуновского движения описывается законом Эйнштейна для среднего квадрата смещения частицы Δх² вдоль любого направления х. Если за время τ между двумя измерениями происходит достаточно большое число столкновений частицы с молекулами, то Δх² пропорционально τ:

Здесь D - коэффициент диффузии, который определяется сопротивлением, оказываемым вязкой средой движущейся в ней частице. Для сферических частиц радиуса а он равен:

где k - постоянная Больцмана, Т - абсолютная температура, η - динамическая вязкость среды. Теория броуновского движения объясняет случайные движения частицы действием случайных сил со стороны молекул и сил трения. Средняя за достаточно большое время сила равна нулю, и среднее смещение броуновской частицы Δх²также оказывается нулевым.

Выводы теории броуновского движения блестяще согласуются с экспериментом. Формулы (1) и (2) были подтверждены опытами Ж. Перрена и Т. Сведберга (1906). Определённые экспериментально на основе этих соотношений постоянная Больцмана и число Авогадро согласуются с их значениями, полученными другими методами.

Теория броуновского движения сыграла важную роль в обосновании статистической механики. Помимо этого, она имеет и практическое значение. Броуновское движение ограничивает точность многих измерительных приборов, а также определяет случайные движения электронов, вызывающие шумы в электрических цепях, случайные движения ионов в электролитах, увеличивающие их электрическое сопротивление и т.п.

Лит. : Эйнштейн А., Смолуховский М. Брауновское движение. М.; Л., 1936; Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. 4-е изд. М., 2004. Т. 4.

В. П. Павлов.