Действие (в физике)

ДЕЙСТВИЕ, физическая величина, выражаемая определённым интегралом и имеющая размерность произведения энергии на время. Различные формы действия позволяют сформулировать интегральные вариационные принципы механики, носящие название наименьшего действия принципов. Стационарное (экстремальное) значение этого интеграла выделяет действительное (фактически происходящее) движение механической системы между двумя положениями в пространстве под действием заданных активных сил из всех кинематически возможных её движений, удовлетворяющих определённым условиям.

Различают действие по Гамильтону и по Лагранжу, фигурирующие в соответствующих принципах наименьшего действия. Выражение для действия по Гамильтону за промежуток времени t-t₀ имеет вид

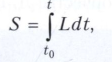
где L = Т - П - функция Лагранжа, Т и П - соответственно кинетическая и потенциальная энергии системы. Величина S используется в принципе наименьшего действия в форме Гамильтона - Остроградского: δS = 0.

Выражение для действия по Лагранжу за промежуток времени t-t₀ имеет вид

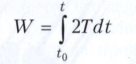
и входит в формулировку принципа наименьшего действия в форме Мопертюи - Лагранжа: δW = 0. Для системы, в которой выполняется закон сохранения механической энергии, величины S и W связаны соотношением S = W - Е·(t - t₀), где Е = Т + П - полная механическая энергия системы.

Величины S и W являются функционалами, зависящими от движения системы, т.к. для их вычисления необходимо задать обобщённые координаты системы q_i (i = 1, ...,n) в виде функций времени t. После этого, выражая Т и П через обобщённые координаты и их производные, можно найти функции Т(t), П(t) и L(t) = Т(t) - П(t), а затем вычислить величины S и W по приведённым выше формулам.

Понятие действия используется также в теории управления, электродинамике, термодинамике и квантовой механике. Элементарный квант действия в квантовой механике h (Планка постоянная) имеет размерность Дж·с.

Лит.: Лурье А. И. Аналитическая механика. М., 1961.