Динамическая игра
ДИНАМИЧЕСКАЯ ИГРА, бескоалиционная игра, в которой игроки совместно управляют движением точки в некотором множестве Х, называемом пространством состояний игры. Динамическая игра может рассматриваться как разновидность позиционных игр, характеризуемая специфической формой как законов перехода от состояния к состоянию, так и выигрышей игроков. Смотри Игр теория.
Процесс динамической игры заключается в последовательном переходе от одного состояния к другому в соответствии с выбором всеми игроками управляющих воздействий; выигрыши игроков определяются всей последовательностью состояний и управлений. Типичными примерами могут служить игры на выживание (разорение), в которых игроки, обладая некоторыми начальными капиталами, последовательно разыгрывают одну и ту же бескоалиционную игру до момента разорения одного из них. Для каждого игрока i, i = 1, ..., n (n - число игроков) и каждой точки х ∈ Х определено множество Si(x) так называемых элементарных стратегий игрока i в этой точке и таким образом определено множество S(x) = S1(x) х…х Sn(x) элементарных ситуаций в точке х. На Х заданы известные каждому из игроков вероятностные распределения
Реклама
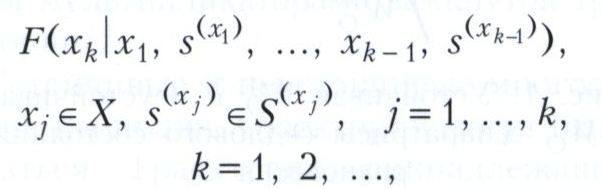
определяющие закон движения управляемой точки. Партия
![]()
в динамической игре определяется индуктивно по следующей схеме. В начальном состоянии х1 каждый игрок выбирает элементарную стратегию si(x1) ∈ Si(x1), i = 1, … n, в результате чего возникает элементарная ситуация s(x1) и игра случайным образом переходит в состояние х2, согласно распределению F(x2|x1, s(x1)). Если определён отрезок партии (x1, s(x1),.., xk-1) и образуется элементарная ситуация s(x k-1), то аналогично игра переходит в состояние xk, в соответствии с распределением F(xk|x1, s(x1),.., xk-1, s(x k-1)). Для каждой партии Р определён выигрыш hi(Р) игрока i. Функции hi(Р), вообще говоря, произвольны, но чаще рассматриваются динамической игрой либо с терминальным выигрышем (игра заканчивается, как только xk оказывается в так называемом терминальном множестве Хγ ⊂ Х и hi(Р) = hi(xk), - последнее состояние в игре), либо с интегральным выигрышем
![]()
Обычно считается, что к очередному моменту выбора элементарной стратегии игроки знают предшествующий отрезок партии. В этом случае чистая стратегия si игрока i есть набор функций
![]()
ставящих в соответствие отрезку партии, заканчивающемуся в х, элементарную стратегию si(x) ∈ Si(x).
Лит.: Воробьев Н. Н. Теория игр для экономистов-кибернетиков. М., 1985.