Диссипативные структуры,

ДИССИПАТИВНЫЕ СТРУКТУРЫ, устойчивые пространственно неоднородные структуры, возникающие в результате развития неустойчивостей в однородной неравновесной диссипативной среде. Термин предложен И. Р. Пригожиным. Примером диссипативных структур могут служить ячейки Рэлея-Бенара (чередование восходящих и нисходящих конвекционных потоков в жидкости), страты в плазме, неоднородные распределения концентраций в химических реакторах, перистые облака и др. В биологии теория диссипативных структур позволяет понять и описать процесс образования сложного организма из оплодотворённой яйцеклетки (морфогенез), пространственно неоднородные распределения особей. Основы общей теории диссипативных структур сформулированы А. М. Тьюрингом в 1952 году.

Простейшие модели диссипативных структур описываются двумя динамическими переменными х, у, зависящими от времени t и одной пространственной координаты r (*):

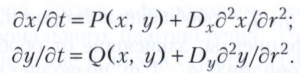
Система (*) описывает кинетику нелинейных процессов (физических, химических, биологических и др.) с учётом миграции компонент х и у (например, за счёт диффузии) в соседние области пространства. Величины D_x и D_y - коэффициенты диффузии, нелинейные функции Р(х,у) и Q(х,у) описывают прирост и убыль компонент х и у. Модели типа (*) называются также уравнениями реакции с диффузией. Образование диссипативных структур возможно при следующих условиях.

1) Одна из переменных (например, х) является«автокаталитической», другая (у) - «демпфирующей». Такие условия выполняются лишь в термодинамически неравновесных открытых системах, которые, согласно терминологии Пригожина, относятся к области «нелинейной термодинамики».

2) Коэффициент диффузии автокатализатора должен быть меньше коэффициента диффузии демпфера (т. е. D_x< D_y).

При выполнении условий 1) и 2) однородное стационарное состояние х = х, у = у может терять устойчивость по отношению к гармоническим возмущениям с определённой длиной волны, соизмеримой с L. Значения параметров системы (*), при которых декремент затухания гармонических возмущений обращается в нуль, называются бифуркационными, а само явление - бифуркацией Тьюринга. Система отбирает из внешних возмущений ограниченное число гармонических мод (в предельном случае одну), которые могут нарастать. Их нарастание стабилизируется нелинейными членами функций Р(х,у) и Q(х,у). При значениях параметров, близких к бифуркационным, образуется плавная гармоническая диссипативная структура При D_x << D_y возникают контрастные диссипативные структуры, которые состоят из узких участков резкого изменения автокаталитической переменной х, чередующихся с широкими участками плавного изменения переменных. При обратном соотношении между коэффициентами диффузии (D_x >> D_y) в системе возникают автоволны. Все изученные модели диссипативных структур разбиваются на два класса, которые можно привести в соответствие с катастрофами типа «складка» и «сборка» (смотри Катастроф теория). Класс диссипативных структур определяется числом экстремумов функции у(х), являющейся решением уравнения Р(х, у) = 0.

В случае одного экстремума («складка») контрастная диссипативная структура состоит из ряда узких «пиков» автокаталитической переменной х(r), разделённых длинными участками плавного изменения обеих переменных. Если имеются два экстремума («сборка»), то возможно образование контрастных диссипативных структур ступенчатой формы, состоящих из широких участков повышенного и пониженного содержания автокатализатора; узкие границы между ними - фронты  резкого  изменения  х(r).

Контрастные диссипативные структур весьма чувствительны к малым неоднородностям пространства, поэтому могут возникать достаточно стабильные непериодические диссипативные структуры, в которых длины плавных участков различны. Теорию диссипативных структур используют для качественного описания явлений самоорганизации в природе; она входит как существенная часть в синергетику и теорию автоволн.

Лит.: Васильев В. А., Романовский Ю. М., Яхно В. Г. Автоволновые процессы в распределенных кинетических системах // Успехи физических наук. 1979. Т. 128. Вып. 4; Николис Г., Пригожин И. Самоорганизация в неравновесных системах. М., 1979; Романовский Ю. М., Степанова Н. В.. Чернавский Д. С. Математическое моделирование в биофизике. 2-е изд. М.; Ижевск, 2004; Чернавский Д. С. Синергетика и информация. М., 2004.