Евклида алгоритм

ЕВКЛИДА АЛГОРИТМ, способ нахождения наибольшего общего делителя двух целых чисел, двух многочленов или общей меры двух отрезков. Описан в геометрической форме Евклидом. Для случая положительных целых чисел а и b таких, что а ≥ b, Евклида алгоритм состоит в следующем. Деление с остатком числа а на число b приводит к результату а = nb + b₁ где частное n является целым положительным числом, а остаток - либо нуль, либо целое положительное число, меньшее b, 0 ≤ b₁ < b. Производится последовательное деление:

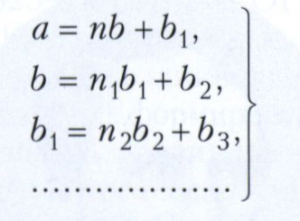
где все n_i - положительные целые числа и 0 ≤ b₁ < b_i-1, i ≥ 2, до тех пор, пока при некотором натуральном k не получится остаток b_k+1 = 0. Остаток b_k+1 можно не писать, поэтому ряд равенств (*) закончится так:

Последний положительный остаток b_k в этом процессе является наибольшим общим делителем чисел а и b. В случае многочленов или отрезков поступают сходным образом. Для несоизмеримых отрезков, то есть отрезков, отношение длин которых иррационально, Евклида алгоритм приводит к бесконечному процессу.