Галуа теория

ГАЛУА ТЕОРИЯ, созданная Э. Галуа теория алгебраических уравнений высших степеней с одним неизвестным, т. е. уравнений вида

основанная на изучении групп перестановок их корней.

Уравнения 2-й, 3-й и 4-й степеней разрешимы в радикалах. Формула х = -р/2 ± √р²/4 - q для решения уравнения х² + рх + q = 0 была известна в глубокой древности. Методы решения уравнений 3-й и 4-й степеней были найдены в 16 веке. Для уравнения 3-й степени вида х³+px + q = 0, к которому можно привести всякое уравнение 3-й степени, решение даётся так называемой формулой Кардано

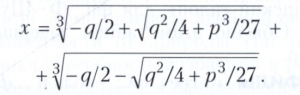
Метод решения в радикалах уравнений 4-й степени был предложен Л. Феррари, оба результата были опубликованы Дж. Кардано в 1545 году.

В 16-18 веках предпринимались попытки найти аналогичные формулы для уравнений 5-й и более высоких степеней. Над этим работали Э. Безу и Ж. Лагранж. В 1801 году К. Гаусс создал полную теорию решения в радикалах двучленного уравнения вида хⁿ = 1, называемого уравнением деления круга; он указал условия для того, чтобы уравнение хⁿ=1 решалось в квадратных радикалах. Последняя задача заключалась в отыскании правильных n-угольников, которые можно построить при помощи циркуля и линейки. Такими оказываются n-угольники при n = 2m и n = 2^mp₁...p_k, где

m = 0, 1, 2 а р₁ ,..., p_k, k= 1, 2, ..., - различные гауссовы простые числа, т. е. простые числа вида 2^2s +1, s = 0, 1, 2, ... (смотри Многоугольник). В 1824 году Н. Абель доказал, что общее уравнение 5-й степени (и тем более общие уравнения более высоких степеней) не решается в радикалах. С другой стороны, Абель дал решение в радикалах для одного класса уравнений, содержащего уравнения произвольно высоких степеней, - так называемых абелевых уравнений.

Таким образом, когда Галуа начал свои исследования, в теории алгебраических уравнений были получены важные результаты, но общей теории, охватывающей все возможные уравнения высоких степеней, ещё не было создано. Нужно было установить необходимые и достаточные условия, которым должно удовлетворять уравнение (1) для того, чтобы оно решалось в радикалах; выяснить, каковы необходимые и достаточные условия для того, чтобы уравнение (1) сводилось к цепи квадратных уравнений, то есть чтобы корни уравнения (1) можно было построить геометрически с помощью циркуля и линейки. Все эти вопросы Галуа решил в «Мемуаре об условиях разрешимости уравнений в радикалах», найденном в его бумагах после смерти и впервые опубликованном Ж. Лиувиллем в 1846 году. Условия разрешимости уравнения (1) в радикалах сформулированы Галуа в терминах групп теории.

Чтобы сформулировать основные результаты Галуа теории, рассмотрим некоторое поле k, содержащее все коэффициенты многочлена f(х). Любое поле К, содержащее k, называется расширением k (обозначение К/k). Его степенью называется размерность К как линейного векторного пространства над к. Если эта размерность конечна, то расширение называется конечным. Поле К = k (α₁, ..., α_n), где α₁, ..., α_n - все корни уравнения (1), то есть минимальное расширение k, в котором f(х) разлагается в произведение линейных множителей, f(х) =  (х-α₁)...(х-α_n), называется полем разложения многочлена f(х) и является конечным расширением k. Если К - поле разложения сепарабельного многочлена, т. е. многочлена, неприводимые множители которого не имеют кратных корней, то К/k называется расширением Галуа. Такому расширению сопоставляется группа Галуа G(К/k), называемая также группой Галуа многочлена f, состоящая из всех автоморфизмов, то есть изоморфизмов поля К на себя, оставляющих неподвижными все элементы k. Порядок этой группы равен степени расширения К/k. Любой её элемент определяет некоторую подстановку корней α₁, ..., α_n многочлена f, поэтому G(К/k) можно рассматривать как подгруппу симметрической группы S_n перестановок n элементов. Основная теорема Галуа теории утверждает, что существует взаимно однозначное соответствие (соответствие Галуа) между всеми промежуточными подполями расширения К/k и всеми подгруппами группы G(К/k). Галуа теория даёт необходимые и достаточные условия разрешимости уравнения (1) в радикалах, т. е. оно разрешимо в радикалах тогда и только тогда, когда его группа Галуа разрешима. В частности, теорема Абеля связана с тем, что общее уравнение (1) имеет в качестве группы Галуа симметрическую группу S_n, которая неразрешима при n≥5. Другое приложение Галуа теории - это полное решение идущей из античности задачи о построении циркулем и линейкой.

В Галуа теории большое значение имеет обратная задача, состоящая в построении расширения Галуа К/k с заданной группой Галуа G. Существует гипотеза о том, что для поля алгебраических чисел k обратная задача разрешима для любой конечной группы G; доказано это только для симметрических, знакопеременных и некоторых типов простых групп. И. Р. Шафаревич доказал (1954), что над любым полем алгебраических чисел существует бесконечно много расширений с заданной разрешимой группой Галуа. Понятия и методы Галуа теории широко используются в алгебраической теории чисел и алгебраической геометрии. Для некоторых типов полей k, включающих поля алгебраических чисел, существует теория (теория полей классов), дающая обзор всех абелевых расширений поля k (расширений с абелевой группой Галуа).

Лит.: Галуа Э. Соч. М.; Л., 1936; Бурбаки Н. Алгебра. Многочлены и поля. Упорядоченные группы. М., 1965; Ленг С. Алгебраические числа. М., 1966; он же. Алгебра. М., 1968; Серр Ж. П. Когомологии Галуа. М., 1968; Artin Е. Galois theory. Ann Arbor, 1971; Ван дер Варден Б. Л. Алгебра. М., 1976; Маtzat В. Konstructive Galoistheorie. В., 1987; Ишханов В. В., Лурье Б. Б., Фаддеев Д. К. Задача погружения в теории Галуа. М., 1990.