Гамильтона-Якоби уравнение

ГАМИЛЬТОНА-ЯКОБИ УРАВНЕНИЕ, дифференциальное уравнение в частных производных 1-го порядка, к интегрированию которого сводится решение уравнений движения голономной консервативной механической системы, представленных в форме Гамильтона уравнений. Гамильтона-Якоби уравнение имеет вид

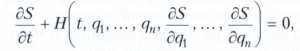
где S - неизвестная функция времени t и обобщённых координат q₁, ..., q_n, называемая действием, Н = Н(t, q_i , p_i) - Гамильтона функция, р₁, ..., р_n - обобщённые импульсы, n - число степеней свободы системы.

Согласно теореме Якоби, полный интеграл Гамильтона-Якоби уравнения, т. е. решение S(t, q_i, p_i) этого уравнения, зависящее от n производных постоянных а₁, ..., а_n и удовлетворяющее условию det([д²S ]/[дq_iда_j] ) ≠ 0,  позволяет получить общее решение уравнений Гамильтона в виде

из соотношений

где b₁, ..., b_n - произвольные постоянные.

Если функция Гамильтона H не зависит от времени, то уравнения Гамильтона допускают интеграл энергии H =  h = а₁ и функцию S можно искать в виде S = - ht + W(q_i, а₂, ..., а_n), где функция W удовлетворяет уравнению

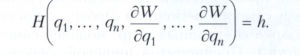
Интегрирование Гамильтона-Якоби уравнения - удобный способ решения многих задач геометрии и теоретической физики, особенно механики, оптики и квантовой механики. Это уравнение нашло также применение в задачах оптимального управления.

А. В. Карапетян.