Информация в математике

ИНФОРМАЦИЯ в математике, общее название понятий, играющих фундаментальную роль в информатике, информации теории, кибернетике, а также в математической статистике. В каждой из этих дисциплин интуитивное представление об информации относительно каких-либо величин или явлений требует своего уточнения и формализации.

Кибернетика изучает машины и живые организмы исключительно с точки зрения их способности воспринимать определённую информацию, сохранять эту информацию в памяти, передавать её по каналам связи и перерабатывать её в сигналы, направляющие их деятельность. В некоторых случаях возможность сравнения различных данных по содержащейся в них информации столь же естественна, как и возможность сравнения плоских фигур по площади: независимо от способа измерения площадей можно сказать, что фигура А имеет не большую площадь, чем В, если А может быть целиком помещена в В. Более глубокий факт - возможность выразить площадь числом и на этой основе сравнивать между собой фигуры произвольной формы - является результатом развития геометрии. Подобно этому фундаментальным результатом теории информации является утверждение о том, что в определённых, весьма широких условиях можно пренебречь качественными особенностями информации и выразить её количество числом. Только этим числом определяются возможности передачи информации по каналам связи и её сохранения в запоминающих устройствах.

Пример 1. Результаты произведённых независимых измерений какой-либо физической величины, хотя и содержат ошибки, дают информацию о её точном значении. Увеличение числа измерений увеличивает эту информацию. Среднее арифметическое результатов наблюдений также содержит некоторую информацию относительно рассматриваемой величины. В математической статистике установлено, что в случае нормального распределения вероятностей ошибок с известной дисперсией среднее арифметическое содержит ту же информацию о точном значении, что и все наблюдения.

Пример 2. Пусть на входе канала связи имеется некоторая случайная величина Х, которая при передаче искажается, в результате чего на выходе получают величину Y = Х + Z, где Z не зависит от Х (в смысле теории вероятностей). Выход Y даёт информацию о входе Х, причём естественно ожидать, что эта информация тем меньше, чем больше рассеяние значений Z.

В приведённых примерах данные можно сравнить по содержащейся в них информацией. Смысл этого сравнения требует уточнения. Это уточнение даётся соответственно математической статистикой и теорией информации.

В основе теории информации лежит предложенный в 1948 году К. Шенноном способ измерения количества информации, содержащейся в одном случайном объекте (событии, величине, функции и т. п.) относительно другого случайного объекта. Этот способ приводит к выражению количества информации числом. Проще всего количество информации определяется в случае, когда случайные объекты являются случайными величинами, принимающими лишь конечное число значений. Пусть Х - случайная величина, принимающая значения х₁, х₂,…, х_n с вероятностями р₁,р₂, ...,р_n, а Y - случайная величина, принимающая значения у₁, у₂ ..., у_m с вероятностями q₁ ,q₂,...,q_m. Тогда количество информации I(Х, Y), содержащееся в Х относительно Y, определяется формулой

где p_ij - вероятность совмещения событий {Х = x_i} и {Y = y_i). Величина I (Х, Х) является энтропией случайной величины Х. Справедливо равенство I (Х, Y) =  I(Y, Х). Величина Ι(Χ, Υ) обладает рядом свойств, которые естественно требовать от меры количества информации. Так, всегда I (Х, Y) ≥ 0, и равенство I (Х, Y) = 0 справедливо тогда и только тогда, когда P_ij = p_iq_j при всех i и j, т. е. когда случайные величины Х и Y независимы. Всегда справедливо неравенство I (Х, У) ≤ I(Y, Y), и равенство справедливо тогда и только тогда, когда Y есть функция от Х (например, Y = Х²).

Понятие энтропии

относится к числу основных понятий теории информации. Количество информации и энтропия связаны соотношением

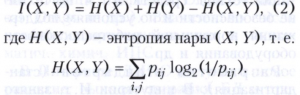
Величина энтропии оценивает сверху среднее число двоичных знаков 0 и 1, необходимое для различения (записи) возможных значений случайной величины при наиболее экономном кодировании, и отличается от него не более чем на 1.

Это обстоятельство позволяет понять роль количества информации (1) при хранении информации в запоминающих устройствах. Если случайные величины Х и Y независимы, то можно считать, что для записи значений Х требуется в среднем Н(Х) двоичных знаков, для записи значений Y требуется Н(Y) двоичных знаков, а для пары (Х, Y) требуется Н(Х) + Н(Y) двоичных знаков. Если же случайные величины Х и Y зависимы, то среднее число двоичных знаков, необходимое для записи пары (Х, Y), оказывается меньше суммы Н(Х) + Н(Y), так как Н(Х, Y)= Н(Х) + Н(Y) - I(Х, Y).

С помощью более глубоких утверждений выясняется роль количества информации (1) в вопросах передачи информации по каналам связи. Основная информационная характеристика, так называемая пропускная способность канала связи, определяется через количество информации.

Если совместное распределение случайных величин Х и Y имеет плотность вероятности, то I(Х, Y) определяется равенством

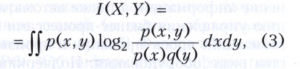
где р(х,у), р(х) и q(у) обозначают соответствующие плотности вероятности. Эта формула получается из (1) с помощью предельного перехода. При этом энтропии Н(Х) и Н(Y) не существуют, но справедлива формула, аналогичная (2),

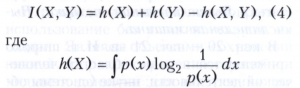
- дифференциальная энтропия случайной величины Х, h(Y) и h(Х, Y) определяются аналогично.

Пример 3. Пусть в условиях примера 2 независимые случайные величины Х и Z имеют нормальные распределения вероятностей с нулевыми средними значениями и дисперсиями, равными соответственно σ²_Х и σ²_Z. Тогда формулы (3) или (4) приводят к равенству

Таким образом, количество информации в принятом сигнале Y относительно переданного сигнала Х стремится к нулю при возрастании уровня помех Z (т.е. при σ²_Z → ∞) и неограниченно возрастает при исчезающе малом влиянии помех (т.е. при σ²_Z → 0).

Особенный интерес для теории информации представляет случай, когда в обстановке примеров 2 и 3 случайные величины Х и Y заменяются случайными функциями (или, как говорят, случайными процессами) Х(t) и Y(t), которые описывают изменение во времени некоторой величины на входе и на выходе передающего устройства. Количество информации в Y(t) относительно Х(t) при заданном уровне помех (шумов) Z(t) может служить критерием качества передающего устройства.

В задачах математической статистики также пользуются понятием информации, введённым Р. Фишером (1921). Однако как по своему формальному определению, так и по своему назначению оно отличается от того, что используется в теории информации. Математическая статистика имеет дело с большим числом результатов наблюдений и заменяет обычно их полное перечисление указанием некоторых сводных характеристик (смотри пример 1). Иногда при такой замене происходит потеря информации, но при некоторых условиях сводные характеристики содержат всю информацию, имеющуюся в полных данных.

Пример 4. Пусть Х₁, Х₂, …, Х_n - результаты n независимых наблюдений некоторой величины, распределённые по нормальному закону с плотностью вероятности

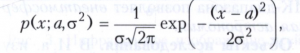
где параметры а и σ² (среднее и дисперсия) неизвестны и должны быть оценены по результатам наблюдений. Достаточными статистиками (так называются функции от результатов наблюдений, содержащие всю информацию о неизвестных параметрах) в этом примере являются среднее арифметическое

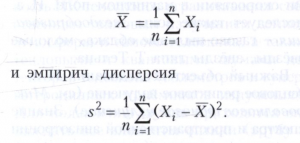
Если параметр σ² известен, то достаточной статистикой для параметра а будет только Х (сравни пример 1). Смысл выражения «вся информация» состоит в следующем. Пусть имеется какая-либо функция неизвестных параметров φ = φ (а, s²) и пусть φ* = φ* (Х₁ , Х₂, ..., Х_n) - какая-либо её оценка, не имеющая систематической ошибки, то есть математическое ожидание φ* совпадает с φ. Пусть качество оценки, т. е. её точность, измеряется, как это обычно делается в задачах математической статистики, дисперсией разности φ* - φ. Тогда существует другая оценка φ**, зависящая не от отдельных величин Х₁ , Х₂, ..., Х_n, а только от сводных характеристик Х и s², не имеющая систематической ошибки и для которой дисперсия разности φ** - φ не превосходит дисперсии разности φ* - φ.

Лит.: Шеннон К. Статистическая теория передачи электрических сигналов //Теория передачи электрических сигналов при наличии помех. М., 1953; Бриллюэн Л. Наука и теория информации. М., 1960; Колмогоров А. Н. Три подхода к определению понятия «количество информации» // Проблемы передачи информации. 1965. Т. 1. № 1; Харкевич А. А. Борьба с помехами. 2-е изд. М., 1965; Черри К. Человек и информация. М., 1972; Яглом А. М., Яглом И. М. Вероятность и информация. 3-е изд. М., 1973; Галлагер Р. Теория информации и надежная связь. М., 1974; Леман Э. Теория точечного оценивания. М., 1991.