Кантора множество

КАНТОРА МНОЖЕСТВО, совершенное множество точек на прямой, не содержащее ни одного отрезка. Построено Г. Кантором (1883) следующим образом (рисунок):

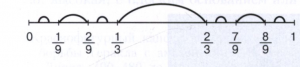
из отрезка [0, 1] удаляется интервал (1/3, 2/3), составляющий его среднюю треть; далее в каждом из оставшихся отрезков [0, 1/3] и [2/3, 1] также удаляются интервалы, составляющие их средние трети; этот процесс удаления интервалов продолжается неограниченно. Кантора множеством называется множество точек отрезка [0, 1], оставшееся после удаления этих интервалов, оно имеет мощность континуума, нулевую меру Лебега (смотри Мера множества) и совпадает с множеством тех чисел, которые записываются с помощью троичных дробей вида 0, а₁ а₂ ..., где каждая из цифр  а₁ а₂ ...   равна 0  или  2.