Кинематика

КИНЕМАТИКА (от греческого ϰίνημα, родительный падеж ϰινήματος - движение), раздел механики, в котором описываются геометрические характеристики движения механического - движения материальных точек и их систем, абсолютно твёрдых тел и т.д. Соответственно выделяют разделы кинематики: кинематика материальной точки, кинематика системы точек, кинематика твёрдого тела и т.д.

Основные понятия кинематики (мгновенная скорость и мгновенное ускорение материальной точки) были введены Г. Галилеем в фундаментальном труде «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению» (1638). Галилей получил строгие математические законы кинематики на основе обобщения экспериментальных данных, установил принцип относительности (смотри Галилея принцип относительности).

Х. Гюйгенс (1672) конкретизировал принципы и понятия кинематики, введённые Галилеем. Работы Гюйгенса послужили базой для создания механики И. Ньютона (1687). В 1765 Л. Эйлер заложил основы кинематики твёрдого тела. В начале 19 века Г. Кориолис дал окончательную формулировку теории относительного движения. С середины 19 века кинематика начала активно использоваться для описания преобразования движения в механизмах и выделилась в самостоятельный раздел теоретической механики.

Кинематика материальной точки. Движение материальной точки описывается по отношению к выбранной системе координат Oxyz. Кинематическими характеристиками движения точки служат векторы r, υ и w, задающие в момент времени t соответственно мгновенное положение, мгновенную скорость и мгновенное ускорение точки: r(t) = {х(t), у(t), z(t)}, υ(t) = dr/dt = {dx/dt, dy/dt, dz/dt} и w(t) =  d²r/dt² = {d²х/dt², d²у/dt², d²z/dt²}. Кроме прямоугольных координат (х, у, z) в кинематике для описания движения точки используются также и криволинейные координаты (цилиндрические, полярные, сферические и т.п.).

Геометрическое место последовательных положений точки в процессе её движения называется траекторией. Соотношение r=r(t) представляет собой параметрическую форму уравнения траектории как некоторой кривой в пространстве. Закон движения материальной точки может быть также определён формой траектории, её положением в пространстве, положением начальной точки О на траектории и положительным направлением отсчёта дуговой координаты s от начальной точки до её текущего значения.

Уравнение s = s(t) определяет закон движения точки по траектории. Скорость материальной точки равна υ = τds,/dt, где τ - единичный вектор касательной к траектории в некоторой точке М. В дифференциальной геометрии вводятся три взаимно ортогональных единичных вектора: τ, n (вектор главной нормали к кривой) и вектор бинормали β = [τ, n]. Векторы τ и n определяют соприкасающуюся плоскость в точке М траектории.

Ускорение точки выражается формулой w(t) = dυ/dt = d²r/dt² = τdυ/dt + nυ²/R. Здесь полное ускорение точки представлено в виде суммы двух взаимно ортогональных векторов - касательного ускорения w_τ (первое слагаемое) и центростремительного ускорения w_n (второе слагаемое), направленного вдоль главной нормали к траектории в сторону центра кривизны, отстоящего от точки М на расстояние R. Проекция вектора ускорения на бинормаль всегда равна нулю.

Для траектории, представляющей собой прямую, в любой её точке расстояние R = ∞; такое движение материальной точки называется прямолинейным. Если величина скорости материальной точки остаётся постоянной [υ(t) = const ≠ 0], то такое её движение называется равномерным. Если касательное ускорение точки постоянно (dυ/dt = const ≠ 0), то такое движение называется равноускоренным.

Путь, пройденный точкой в её движении вдоль траектории, определяется как интеграл по времени от модуля скорости. Величина пути монотонно возрастает, в то время как координата точки может то возрастать, то уменьшаться. Например, при незатухающих колебаниях математического маятника путь колеблющейся материальной точки непрерывно возрастает, а её дуговая координата принимает значения, ограниченные амплитудой А колебаний (от -А до +А).

Кинематика относительного движения. Система координат Oxyz, относительно которой рассматривается движение материальной точки М, может быть связана с некоторым телом, которое само движется относительно неподвижной системы O₁x₁y₁z₁. В этом случае скорость и ускорение точки М относительно системы Oxyz называют относительными и обозначают соответственно υ_отн и w_oтн. Движение той же материальной точки относительно системы O₁x₁y₁z₁ называют абсолютным, его скорость и ускорение обозначают  υ_абс и w_aбc. При отсутствии относительного движения (υ_отн = 0) точка М переносится движущимся телом, с которым связана система Oxyz, и её скорость совпадает со скоростью υ_пер той точки N тела, в которой в данный момент находится точка М: rN(t) = rM(t), но не тождественно (т. к. речь идёт о независимых точках). Вектор υ_пер = drN/dt называется переносной скоростью или скоростью переносного движения. Формула υ_абс =υ_отн+ υ_пер выражает так называемую теорему сложения скоростей. Ускорение точки N называют переносным и обозначают w_пep. Сложение ускорений описывается теоремой Кориолиса: w_aбc = w_oтн + w_пep + w_Kop. Здесь дополнительное слагаемое w_Kop (Кориолиса ускорение) возникает в том случае, если система Oxyz вращается относительно системы O₁x₁y₁z₁: w_Кор = 2[ω, υ_отн], где ω - вектор угловой скорости подвижной системы координат.

Кинематика систем связанных точек и тел. Машины, механизмы и другие объекты техники часто моделируют системой связанных материальных точек и тел (смотри Связи механические). В системе со связями положения и скорости различных точек системы не могут быть заданы произвольно. Первой задачей кинематики таких систем является формализация связей, которые записывают в виде уравнений связей - полного набора независимых соотношений между координатами точек системы. Вторая задача кинематики систем связанных точек и тел сводится к сокращению числа величин, необходимых для полного описания движения объекта. Для этого из общего числа величин исключают те, которые выражаются через другие величины при помощи уравнений связей. Последняя задача нередко решается с помощью подходящего выбора обобщённых координат.

Обе задачи кинематики допускают неоднозначные решения. Из всех решений выбираются такие, которые позволяют придать системе дифференциальных уравнений движения объекта наиболее удобную форму. В теории машин и механизмов, кроме того, необходимо связать входные и выходные характеристики движения (смотри Кинематика механизмов).

Кинематика твёрдого тела. В этом разделе кинематики рассматриваются различные типы движений абсолютно твёрдого тела. Под абсолютно твёрдым телом понимают систему материальных точек, взаимное положение которых не изменяется. Основная задача кинематики твёрдого тела - определение скоростей и ускорений всех его точек.

С геометрической точки зрения движение абсолютно твёрдого тела относительно неподвижной системы координат O₁x₁y₁z₁ с началом в точке О₁ эквивалентно движению связанной с этим телом системы Oxyz с началом в произвольно выбранной точке О тела. Положение тела однозначно определяется положением трёх его точек, не лежащих на одной прямой. Положение трёх точек в системе O₁x₁y₁z₁ задаётся с помощью девяти координат, на которые наложены три условия постоянства взаимных расстояний между точками. Это сокращает число независимых величин (определяющих максимальное число степеней свободы тела) до шести. Дополнительные ограничения на движение тела уменьшают число степеней свободы и определяют тип движения тела. Так, при фиксированных координатах указанных точек тело находится в состоянии покоя относительно системы O₁x₁y₁z₁.

Поступательное движение тела. Движение твёрдого тела называют поступательным, если каждый прямолинейный отрезок, состоящий из точек тела, перемещается параллельно самому себе. В этом случае оси системы координат, связанной с телом, можно расположить сонаправленно осям неподвижной системы. Скорость и ускорение любой точки тела равны соответственно скорости и ускорению точки О (начала системы координат, связанной с телом). Точка О может двигаться как по прямой, так и по плоской или пространственной кривой. Например, вагон поезда на прямом участке пути движется поступательно и прямолинейно. Кабина колеса обозрения тоже движется поступательно, но её точки описывают окружности.

Тело, движущееся поступательно, имеет три степени свободы (столько же, сколько у материальной точки), для описания его движения достаточно задать три независимые координаты.

Вращение тела вокруг оси. При вращательном движении тела связанная с ним система координат изменяет свою ориентацию относительно неподвижной системы, т. е. совершает поворот. Наиболее простой случай вращательного движения - вращения тела вокруг неподвижной оси. Для описания такого движения три точки тела выбирают следующим образом: две точки - на оси вращения, а третью - вне этой оси. При движении тела две первые точки не изменяют своего положения относительно неподвижной системы координат, а третья точка описывает окружность с центром на оси вращения. Таким образом, тело имеет одну степень свободы, его положение определяется одной координатой - углом φ между текущим положением плоскости трёх выбранных точек и плоскостью Ox₁z, определяющей положение неподвижной системы координат. Уравнение φ = φ(t) задаёт закон вращения тела вокруг неподвижной оси. Кинематическими характеристиками этого движения служат угловая скорость ω(t) = dφ/dt и угловое ускорение   ε = dω/dt = d²φ/dt².

Скорость υ_N произвольной точки N тела, не принадлежащей оси вращения, направлена по касательной к соответствующей окружности и равна υ_N = ωR_N, где R_N - расстояние от точки N до оси вращения. Вектор ускорения w_N  точки может быть представлен в виде суммы векторов касательного ускорения w_τ и центростремительного ускорения w_n, причём     w_τ = εR_n = dυ_N/dt, w_n =ω²R_N = υ²_N  /R_N.

Данный раздел кинематики твёрдого тела используют для описания различных механизмов, содержащих вращающиеся элементы (роторы, турбины, колёса).

При более сложных вращательных движениях учитывается прецессия оси вращения. В этом случае вращательное движение тела может быть представлено суперпозицией двух простых вращений: тело вращается вокруг своей оси Oz, которая в свою очередь вращается вокруг неподвижной оси Oz₁. Тогда ориентация тела в пространстве определяется тремя координатами - так называемыми Эйлера углами [ψ(t) - угол прецессии, φ(t) - угол собственного вращения, θ - постоянный угол нутации].

Вращение тела вокруг неподвижной точки. При произвольном вращении тела вокруг неподвижной точки О все три угла Эйлера зависят от времени, причём движение тела нельзя свести к двум простым вращениям. Как показал Л. Эйлер, для описания данного движения можно найти такой вектор ω (называемый мгновенной угловой скоростью тела), что скорость υ_N точки N тела определяется формулой υ_N= [ω, r_N]. Те точки тела, для которых векторы r_N и ω коллинеарны, образуют мгновенную ось вращения тела (мгновенная скорость этих точек равна нулю). Вектор ω = {ω_х, ω_у, ω_z} представляет собой геометрическую сумму трёх векторов: е₁dψ/dt - угловая скорость прецессии (орт е₁ неизменен в неподвижной системе координат), е₂dφ/dt - угловая скорость собственного вращения (орт е₂ неизменен относительно тела), е₃dθ/dt - угловая скорость нутации (орт е₃ вращается вокруг е₁). Движение твёрдого тела относительно неподвижной точки описывается следующими кинематическими Эйлера уравнениями:

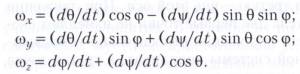
Кроме углов Эйлера для описания вращательного движения тела могут быть использованы и другие параметры: углы Крылова, параметры Родрига - Гамильтона и т. п. Ускорение w_N точки N тела вычисляется по формуле Ривальса: w_N =  [dω/dt, r_Ν] + [ω, [ω, r_N]].

Произвольное движение тела. Произвольное движение твёрдого тела можно разложить на две составляющие: поступательное движение со скоростью υ_О некоторой точки О тела и вращение вокруг этой точки с угловой скоростью ω. Замена точки О на другую точку, например точку N, вносит изменение в описание этого же движения. Вообще говоря, изменяется направление и величина скорости υ_N поступательного движения, но не изменяется угловая скорость ω вращения, совершаемого теперь вокруг точки N. Если ω ≠ 0 и (υ₀, ω) ≠ 0, в теле существует множество точек, для которых векторы υ и ω коллинеарны. Эти точки образуют мгновенную винтовую ось движения тела (смотри Винтовое движение).

Плоскопараллельное движение тела. Тело совершает плоскопараллельное движение, если скорости всех его точек в любой момент времени параллельны некоторой неподвижной плоскости. Спроектировав тело на эту плоскость, получим плоскую фигуру, движение которой по плоскости эквивалентно движению тела. Если в этом движении ω(t) ≠ 0, то вектор ω ортогонален указанной плоскости, (υ_О, ω) ≠ 0 и ось мгновенного винта пересекает фигуру в мгновенном центре вращения. Если ω = 0, но υ_О≠0, то тело находится в состоянии мгновенно поступательного движения.

Кинематика  сплошных сред (деформируемого тела, несжимаемой и сжимаемой жидкости) требует более сложных процедур описания: рассматривается общая теория деформаций, определяются так называемые уравнения неразрывности и т. д. (смотри Механика сплошной среды, Механика жидкости и газа).

Лит.: Эйлер Л. Основы динамики точки. М.; Л., 1938; Жуковский Н. Е. Теоретическая механика. 2-е изд. М.; Л., 1952; Лурье А. И. Аналитическая механика. М., 1961; Бухгольц Н. Н. Основной курс теоретической механики. 9-е изд. М., 1972. Ч. 1; Курс теоретической механики / Под редакцией К. С. Колесникова. 2-е изд. М., 2002. Т. 1; Тарг С. М. Краткий курс теоретической механики. 17-е изд. М., 2007.