Комбинаторные числа и много­члены

КОМБИНАТОРНЫЕ ЧИСЛА И МНОГОЧЛЕНЫ, общее название специальных чисел и многочленов, которые играют важную роль в решении комбинаторных задач. Как правило, комбинаторные числа имеют наглядную комбинаторную интерпретацию (зачастую не единственную), выражаемую в терминах числа способов выбора и расположения элементов некоторого, обычно конечного, множества, приводящих к конфигурациям данного класса или числа объектов из некоторого множества объектов, обладающих тем или иным выделенным свойством.

Простейшими примерами комбинаторных чисел являются числа сочетаний, размещений и перестановок. Если имеется множество из N различных элементов, то его подмножества называются сочетаниями, число различных сочетаний размера k равно

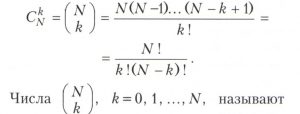
биномиальными коэффициентами, поскольку они входят в формулу Ньютона бинома. Упорядоченные наборы из различных элементов множества N называются размещениями, число различных размещений размера k равно

В случае N = k размещения называются перестановками, число всех перестановок из N элементов равно PN = N!, где N! =N(N-1).. .2·1. Сочетания, размещения и перестановки используются в различных разделах математики.

Если допускаются повторения элементов, то число всех сочетаний размера k из N различных элементов равно Ck_N-k+1, а число всех упорядоченных наборов размера k равно N^k. Эти числа используют при нахождении вероятностей различных событий при классическом определении вероятности (смотри Вероятностей теория). Например, если имеется урна с N шарами, занумерованными числами 1, 2, ..., N, причём шаров с номерами 1, 2, ..., М белого цвета, а остальные - чёрного, то вероятность получить ровно m белых шаров при случайном выборе из урны n шаров равна

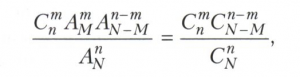
если выбор производится без возвращения шаров, и равна

при выборе с возвращением.

Из числа более специальных комбинаторных чисел наиболее часто используются так называемые числа Каталана

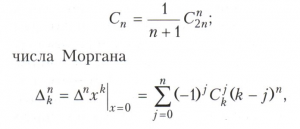
где Δ - оператор разности Δf(х) = f(х + 1) - f(х); числа Стирлинга S(n, k) и σ(n, k) соответственно 1-го и 2-го рода; числа Белла

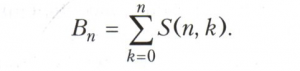
Все эти числа, как правило, имеют наглядные комбинаторные интерпретации. Так, например, число Каталана С_n равно числу векторов (ε₁,..., ε_2n), ε_i= +1,

i = 1, ...,2 n, таких, что ∑^k_i=1ε_i  ≥0,

k=1...... 2n- 1,  ∑²ⁿ_i=1ε_i = 0;

число Мор­гана Δⁿ_k равно числу отображений f множества А из k элементов на множество В из n элементов, т. е. таких отображений, что f(А) = f(В); число Белла В_n есть число различных разбиений множества из n элементов на непересекающиеся подмножества.

При исследовании свойств комбинаторных чисел широко используют производящие функции, рекуррентные соотношения и конечно-разностные уравнения. Во многих случаях на рассматриваемом множестве объектов удаётся построить подходящую вероятностную модель и тем самым комбинаторную задачу перечислительного характера сформулировать как задачу изучения распределения вероятностей соответствующей случайной величины. Такая интерпретация даёт возможность применять при изучении комбинаторных чисел различные методы теории вероятностей.

Под комбинаторными многочленами понимают производящие функции комбинаторных чисел или производящие функции этих чисел с некоторыми весами. Например, производящей функцией чисел сочетаний C^k_N, k = 0,1,..., N, является бином Ньютона

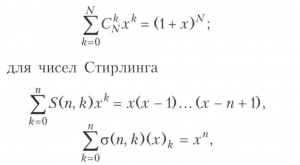
где (x)k = х(х-1 )...(х - k + 1), k = 0,1, ..., n.

Лит.: Сачков В. Н. Комбинаторные методы дискретной математики. М., 1977; Платонов М. Л. Комбинаторные числа класса отображений и их приложения. М., 1979; Кузьмин О. В. Обобщенные пирамиды Паскаля и их приложения. Новосиб., 2000.