Комбинаторные задачи классиче­ские

КОМБИНАТОРНЫЕ ЗАДАЧИ КЛАССИЧЕСКИЕ, задачи выбора и расположения элементов конечного множества, в которых на выбор и расположение налагаются те или иные условия. К комбинаторным задачам классическим можно отнести многие задачи развлекательного характера типа головоломок.

Одной из комбинаторных задач классических, упоминающейся ещё в мифах Древнего Востока, является построение магических квадратов, т. е. расположение первых n² натуральных чисел в квадрате n х n так, чтобы все суммы чисел по строкам, столбцам и диагоналям были равны одному и тому же числу. Например,

4  9  2

3  5  7

8  1  6

- магический квадрат при n = 3. Известен ряд методов построения таких квадратов. Задача о нахождении формулы для числа магических квадратов порядка n для любого натурального n до сих пор не решена.

Ряд комбинаторных задач классических был рассмотрен Л. Эйлером. Одна из них - задача о 36 офицерах, в которой требуется расположить в ячейках квадрата 6х6 (каре) 36 офицеров 6 различных воинских званий и 6 различных полков так, чтобы каждая колонна и каждая шеренга содержали одновременно одного и только одного офицера каждого звания и каждого полка. Эта задача эквивалентна задаче о существовании пары ортогональных латинских квадратов порядка 6. Эйлер высказал гипотезу о том, что ортогональных латинских квадратов порядков n = 4k + 2, k=1, 2,..., не существует. В 1900 году французский математик Г. Тарри подтвердил эту гипотезу для n = 6 и тем самым доказал, что задача о 36 офицерах не имеет решения. В 1959 году индийским математиком С. Човлой, венгерским математиком П. Эрдёшем и немецким математиком Г. Штраусом была доказана теорема о существовании пары ортогональных латинских квадратов для каждого n = 4k + 2, k = 2, 3,...

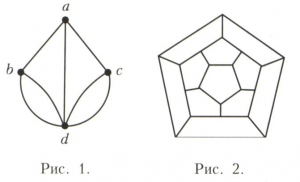
Другая задача, рассмотренная Эйлером, - задача о кёнигсбергских мостах, формулируемая следующим образом. В городе имеется 7 мостов, соединяющих берега реки и 2 острова, расположенные на ней. Спрашивается, можно ли обойти все мосты, проходя по каждому только 1 раз, и возвратиться в исходную точку. В терминах графов теории эта задача формулируется следующим образом. Полагая, что вершины соответствуют районам суши, а рёбра - мостам, задачу о кёнигсбергских мостах можно сформулировать в виде вопроса о возможности последовательного обхода графа, изображённого на рисунке 1, проходя его рёбра по одному разу и возвращаясь в исходную точку. Если в графе такой обход возможен, то говорят, что он обладает эйлеровым циклом. Эйлер установил, что такой цикл в графе существует тогда и только тогда, когда он является связным и число рёбер, инцидентных каждой вершине, чётно. Т. к. граф на рисунке 1 не удовлетворяет этому требованию, то задача о кёнигсбергских мостах неразрешима. Она неразрешима и в том случае, если отбросить требование совпадения точек начала и конца обхода; в этом случае ставится вопрос о существовании эйлеровой цепи в графе. Граф обладает эйлеровой цепью тогда и только тогда, когда он связен и число вершин, инцидентных нечётному числу рёбер, равно 0 или 2. Граф на рисунке 1 не удовлетворяет и этому условию.

В 1859 году У. Гамильтон предложил головоломку «Кругосветное путешествие», состоящую в отыскании такого пути, проходящего через все вершины (их можно интерпретировать как города) графа, изображённого на рисунке 2, чтобы посетить каждую вершину только один раз и вернуться в исходную вершину. Пути в графах, обладающие таким свойством, называются гамильтоновыми циклами. Необходимые и достаточные условия существования гамильтонова цикла в графе неизвестны. Задача о гамильтоновых циклах в графе получила различные обобщения. Одно из них - задача коммивояжёра, имеющая ряд приложений в исследовании операций, в частности при решении некоторых транспортных проблем. Она состоит в следующем: имеется некоторое количество городов, расстояния между которыми известны; нужно найти кратчайший замкнутый путь, проходящий через все города.

В 1847 году английский математик Т. Киркман поставил и решил задачу о 15 школьницах, которые должны гулять ежедневно пятью группами по трое в каждой группе. Необходимо так составить расписание для их прогулок, чтобы каждая школьница в течение семи дней точно один раз попадала в одну группу с каждой из остальных. Эта задача связана с задачей, поставленной швейцарским математиком Я. Штейнером (1853), о построении систем троек. Системой троек Штейнера порядка v называется такой набор троек из множества, содержащего v элементов, что каждая пара элементов входит точно в одну тройку. Системы троек Штейнера описаны для v ≤15. Оказывается, что для v = 3, 7, 9 системы троек единственны с точностью до эквивалентности (до перестановки v элементов и перестановки троек); для v = 13 существуют две неэквивалентные системы троек; при v =15 таких троек 80. Для v>15 число различных систем троек Штейнера неизвестно.

Классическая задача о встречах состоит в следующем. Имеются две одинаковые колоды карт из n различных карт каждая. Необходимо определить число расположений карт D_nr, г = 0,1,...,n, во второй колоде таких, что при сравнении соответствующих карт первой и второй колоды число совпадений равно r. Частный случай этой задачи при r = 0 впервые был сформулирован французским учёным П. де Монмором в начале 18 века.

К комбинаторной задаче классической относится так называемая задача о супружеских парах, которая состоит в определении числа рассаживаний n супружеских пар на 2n местах за круглым столом так, чтобы ни один муж не сидел рядом со своей женой.

Задача о числе разбиений натурального числа n на слагаемые появилась в письме Г. В. Лейбница к Я. Бернулли (1669). Разработка методов решения задач такого типа была осуществлена Эйлером, который эффективно использовал для этой цели производящие функции.

Классическая задача размещения состоит в определении числа С_nm(r) способов размещения m различных предметов в n различных ячейках с заданным числом r пустых ячеек. Оказывается, что

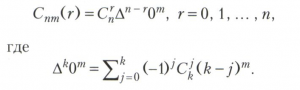
Эта задача имеет различные теоретико-вероятностные приложения. При этом в основном получаются асимптотические результаты, когда m и n неограниченно возрастают.

Лит.: Риордан Дж. Введение в комбинаторный анализ. М., 1963; Постников М. М. Магические квадраты. М., 1964; Холл М. Комбинаторика. М., 1970; Сачков В. Н. Введение в комбинаторные методы дискретной математики. 2-е изд. М., 2004; Харари Ф. Теория графов. 3-е изд. М., 2006.