Комбинаторный анализ

КОМБИНАТОРНЫЙ АНАЛИЗ (комбинаторная математика, комбинаторика), раздел математики, посвящённый решению задач о выборе и расположении в соответствии с заданными правилами элементов некоторого, обычно конечного, множества. Каждое такое правило определяет способ построения некоторой конструкции, состоящей из элементов исходного множества, которая называется комбинаторной конфигурацией. Можно сказать, что целью комбинаторного анализа является изучение комбинаторных конфигураций, в частности изучаются вопросы их существования, алгоритмы построения, решаются задачи на перечисление. Примерами комбинаторных конфигураций являются перестановки, размещения, сочетания (смотри Комбинаторные числа и многочлены), блок-схемы и латинские квадраты.

Развитие комбинаторного анализа шло параллельно с развитием других разделов математики, таких как алгебра, теория чисел, теория вероятностей, с которыми комбинаторный анализ  тесно связан. Ещё математики Древнего Востока знали формулу, выражающую число сочетаний через биномиальные коэффициенты, и формулу Ньютона бинома с натуральным показателем n. С мистическими целями изучались магические квадраты 3-го порядка. Становление комбинаторного анализа как раздела математики связано с работами Б. Паскаля и П. Ферма по азартным играм. Эти работы, заложившие основы элементарной теории вероятностей, содержали принципы определения числа комбинаций элементов конечного множества. Большой вклад в развитие комбинаторных методов был сделан Г. В. Лейбницем, Я. Бернулли, Л. Эйлером. С 1950-х годов интерес к комбинаторному анализу возродился в связи с бурным развитием дискретной математики, информатики, информации теории, кибернетики и планирования эксперимента. На формирование направлений исследований в комбинаторном анализе оказывают влияние, как выбор объектов исследований, так и цели исследования, зависящие от сложности изучаемых объектов. Для сложных комбинаторных конфигураций основными целями исследований являются выяснение условий их существования и разработка алгоритмов построения. Ещё одно направление исследований в комбинаторном анализе связано с теоремами выбора. В основе многих результатов этого направления лежит теорема Холла о существовании систем различных представителей (трансверсалей) семейства подмножеств некоторого множества, которые определяются следующим образом. Пусть Т = {t₁, t₂,..,t_m} – некоторое множество S = {S₁,S₂,...,S_n} - некоторое семейство его подмножеств. Набор R = {t_i1, t_i2,..., t_in} различных элементов множества Т называется системой различных представителей (c.p.n.) семейства S, если t_ij ∈ S_j; элемент t_ij называется представителем множества S_j, j = 1,2,..., n. Теорема Холла о c.p.n. состоит в том, что семейство S имеет c.p.n. тогда и только тогда, когда объединение каждых k множеств из S содержит, по крайней мере, k различных элементов, k = 1, 2,..., n.

Пусть

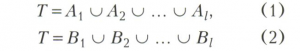
- два разбиения множества Т, в которых ни одно из подмножеств Т не пусто. Набор R ={t_i1,t_i2,...,t_ij} называется системой общих представителей (c.p.n.) разбиений (1) и (2), если R есть c.p.n. как для семейства А = {A₁, А₂, ...,A_l}, так и для семейства В = {В₁, В₂,..., B_l}. Теорема о c.p.n. состоит в том, что разбиения (1) и (2) имеют c.p.n. тогда и только тогда, когда объединение каждых k множеств из семейства А содержит не более k множеств из семейства В, k = 1, 2,...,l. Теореме Холла о c.p.n. эквивалентна теорема Кёнига о (0, 1)-матрице, которая утверждает, что минимальное число линий (строк и столбцов), содержащих все единицы, равно максимальному числу единиц, которые могут быть выбраны так, что среди них нет двух единиц, расположенных на одной и той же линии.

Значительную часть комбинаторного анализа составляют перечислительные задачи, решением которых является метод перебора комбинаторных конфигураций из данного класса и определение их числа. Примерами решения перечислительных задач являются следующие результаты. Число подстановок степени n с k циклами равно |S(n, k) | , где S (n, k) - числа Стирлинга 1-го рода, определяемые равенствами

число разбиений множества из n элементов на k подмножеств равно числу Стирлинга 2-рода

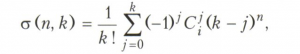
где C^j_i - число сочетаний из i по j; число размещений m различных предметов по n различным ячейкам при условии, что пустых ячеек нет, равно п!σ(m,n). Для решения некоторых перечислительных задач используется перманент матрицы, который для матрицы А = || a_ij||, i=1,..., n, j = 1, ...,m, n ≤ m, определяется равенством

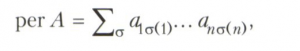
где суммирование производится по всем инъективным отображениям σ множества {1,..., n} в множества {1,..., m}, т. е. таким отображениям, при которых различные элементы из {1,..., n} имеют различные образы в {1,..., m}. Так, число трансверсалей некоторого семейства из n подмножеств конечного множества, состоящего из m элементов, равно перманенту соответствующей матрицы инцидентности (смотри, например, Графов теория).

При решении перечислительных задач комбинаторного анализа существенную роль играет формализация понятия неразличимости объектов. Использование для этих целей понятия эквивалентности объектов относительно некоторой группы подстановок в сочетании с применением метода производящих функций положено в основу так называемой теории перечисления Пойа.

Лит.: Сачков В. Н. Комбинаторные методы дискретной математики. М., 1977; Рыбников К. А. Введение в комбинаторный анализ. 2-е изд. М., 1985.