Конические сечения

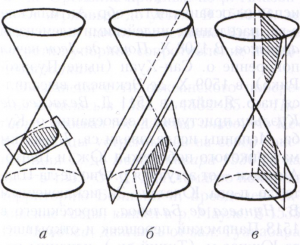
КОНИЧЕСКИЕ СЕЧЕНИЯ, линии, которые получаются сечением прямого кругового конуса плоскостями, не проходящими через его вершину. Существуют конические сечения трёх типов. 1) Секущая плоскость пересекает все образующие конуса в точках одной его полости (рис., а); линия пересечения есть замкнутая овальная кривая - эллипс, окружность как частный случай эллипса получается, когда секущая плоскость перпендикулярна оси конуса. 2) Секущая плоскость параллельна одной из касательных плоскостей конуса (рис., б); в сечении получается незамкнутая, уходящая в бесконечность кривая - парабола, целиком лежащая на одной полости. 3) Секущая плоскость пересекает обе полости конуса (рис., в); линия пересечения - гипербола - состоит из двух одинаковых незамкнутых, простирающихся в бесконечность частей (ветвей гиперболы), каждая из которых лежит на своей полости конуса.

В аналитической геометрии конические сечения - действительные, нераспадающиеся линии второго порядка. В тех случаях, когда коническое сечение имеет центр симметрии (центр), то есть является эллипсом или гиперболой, его уравнение в декартовой системе координат может быть приведено (путём перенесения начала координат в центр) к виду а₁₁х² + 2а₁₂ху + а₂₂y² = а₃₃, где а₁₁, а₁₂, а₂₂, а₃₃ - постоянные. Уравнения этих кривых могут быть приведены к более простому виду

Aх² + Βу² = С,                                           (*)

если за направления осей координат выбрать так называемые главные направления - направления главных осей (осей симметрии) конического сечения. Если постоянные А и В имеют одинаковые знаки (совпадающие со знаком С), то уравнение (*) определяет эллипс; если А и В разного знака, то - гиперболу.

Уравнение параболы привести к виду (*) нельзя. При надлежащем выборе осей координат (одна ось координат - единственная ось симметрии параболы, другая - перпендикулярная к ней прямая, проходящая через вершину параболы) её уравнение можно привести к виду у² = 2 рх.

Конические сечения были известны математикам Древней Греции. То, что эллипс, гипербола и парабола являются сечениями конусов, открыто Менехмом (около 340 года до нашей эры). Наиболее полное сочинение, посвящённое этим кривым, - «Конические сечения» Аполлония Пергского (около 200 года до нашей эры). Дальнейшее развитие теории конических сечений связано с созданием в 17 веке проективного (Ж. Дезарг, Б. Паскаль) и координатного (Р. Декарт, П. Ферма) методов. При надлежащем выборе системы координат (ось абсцисс - ось симметрии конического сечения, ось ординат - касательная к вершине конического сечения) уравнение конического сечения приводится к виду у² = 2рх + λх², где р и λ - постоянные, р≠0. При λ = 0 это уравнение задаёт параболу, при λ<0 - эллипс, при λ>0 -гиперболу. Это свойство конического сечения, содержащееся в последнем уравнении, было известно древнегреческим геометрам и послужило для Аполлония Пергского поводом присвоить отдельным типам конического сечения названия, сохранившиеся до сих пор: слово «парабола» означает приложение (т. к. в греческой геометрии превращение прямоугольника данной площади у² в равновеликий ему прямоугольник с данным основанием 2р называется приложением данного прямоугольника к этому основанию); слово «эллипс» - недостаток (приложение с недостатком); слово «гипербола» - избыток (приложение с избытком).

Стереометрическое определение конического сечения можно заменить планиметрическими определениями этих кривых как множеств точек на плоскости. Так, например, эллипс является множеством точек, для которых сумма расстояний до двух данных точек (фокусов) имеет одно и то же значение. Можно дать и другое планиметрическое определение конического сечения, охватывающее все три типа этих кривых: коническое сечение - множество точек, для каждой из которых отношение расстояний до данной точки (фокуса) к расстоянию до данной прямой (директрисы) равно данному положительному числу (эксцентриситету) е. При е<1 коническое сечение - эллипс; при е > 1 - гипербола; при е = 1 - парабола.

Интерес к коническому сечению всегда поддерживался тем, что эти линии часто встречаются в описаниях различных явлений природы и в человеческой деятельности. Конические сечения приобрели особое значение после того, как И. Кеплер (1609) установил с помощью наблюдений, а И. Ньютон (1687) теоретически обосновал законы движения планет (один из которых утверждает, что планеты и кометы Солнечной системы движутся по коническим сечениям, в одном из фокусов которого находится Солнце).

Лит.: Варден Б. Л. ван дер. Пробуждающаяся наука. 2-е изд. М., 2006; Александров П. С. Лекции по аналитической геометрии. 2-е изд. М., 2008.