Краевые задачи

КРАЕВЫЕ ЗАДАЧИ, задачи, в которых из некоторого класса функций, определённых в данной области, требуется выделить ту, которая удовлетворяет заданным на границе (крае) этой области условиям. Функции, описывающие реальные процессы (физические, химические и др.), как правило, представляют собой решения уравнений математической физики, выведенных из общих законов, описывающих эти процессы. Когда рассматриваемые уравнения допускают целые семейства решений, дополнительно задают так называемые краевые (граничные) или начальные условия, позволяющие однозначно выделить нужное решение. Краевые условия задаются в граничных точках области, где ищется решение, начальные условия могут задаваться на определённом множестве точек внутри области. Например, уравнение

(1)

имеет бесконечное множество решений

u(х₁, х₂) = f(х₁ + х₂) + g(х₁ - х₂), где f и g - произвольные дважды непрерывно дифференцируемые функции. Однако в прямоугольнике {0 ≤ х₁ ≤ l, - а ≤ х₂ ≤ а} плоскости с прямоугольными декартовыми координатами х₁, х₂ уравнение (1) имеет единственное решение u(х₁, х₂), удовлетворяющее краевым

u(0, х₂) = 0, (2)

u(l, х₂) = 0, - а ≤ х₂ ≤ а,

и начальным

u(х₁, 0) = φ(х₁),

(3)

условиям. При этом функции φ и ψ (соответственно дважды и один раз непрерывно дифференцируемые) считаются заданными. Если переменная х₂ есть время t, то решение u(х₁,t) уравнения (1), удовлетворяющее условиям (2) и (3), описывает колебание упругой струны длины l с концами, закреплёнными в точках (0, 0) и (0, l). Задача нахождения решения уравнения (1) при условиях (2) и (3) даёт пример так называемой смешанной задачи.

Краевыми называются задачи, для которых в заданной области G пространства независимых переменных х = (х₁,...,x_n) ищется решение u(х) = u(х₁,...,x_n) уравнения

Du(х) = 0, х ∈ G, (4)

при этом требуется, чтобы искомая функция u(х) на границе S области G удовлетворяла краевому (граничному) условию

Вu(х) = 0, х ∈ S, (5)

где D и В - заданные операторы, причём, как правило, D - дифференциальный или интегро-дифференциальный оператор. Граница S называется носителем краевых данных (5).

В случае, когда операторы D и В линейны, краевая задача (4), (5) называется линейной. В предположениях, что S является (n - 1) - мерной гиперповерхностью, D - линейным дифференциальным оператором 2-го порядка,

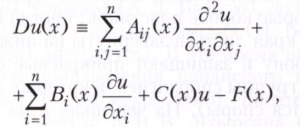
а

Bu(х) ≡ u(х) - f(х),

где A_ij, B_t, С, F, f - заданные функции, задача (4), (5) называется первой краевой задачей, или задачей Дирихле. Если же

где a_i, i=1,...,n, f - заданные функции, то задача (4), (5) называется задачей с наклонной (косой) производной. В частности, когда вектор (а₁,...,a_n) совпадает с конормалью к S, т. е. a_i = A_ij(х)v_j, i,j= 1, ...,n, где (v₁,..., v_n) - внешняя нормаль к S, задача с наклонной производной носит название второй краевой задачи, или задачи Неймана. Задача Дирихле (Неймана) называется однородной, если F(х) ≡ 0, f(х) ≡ 0.

Задачи Дирихле и Неймана хорошо исследованы в ограниченных областях с достаточно гладкой границей в случае, когда оператор D с действительными коэффициентами удовлетворяет условию равномерной эллиптичности, т. е. когда существуют положительные числа k₀ и k₁ такие, что

для любых действительных чисел λ₁,..., λ_n и любого х ∈ G. При достаточной гладкости коэффициентов операторов D и В и равномерной эллиптичности оператора D справедливы следующие утверждения: число k линейно независимых решений однородной задачи Дирихле (Неймана) конечно; для разрешимости задачи Дирихле (Неймана) необходимо и достаточно, чтобы функции F(х) и f(х) были подчинены дополнительным ограничениям типа условий ортогональности, число которых равно k; при выполнении условия С(х) ≤ 0, х ∈ G, задача Дирихле имеет единственное решение; в области G достаточно малого диаметра задача Дирихле имеет единственное решение; при однозначной разрешимости задачи Дирихле (Неймана) малое изменение краевых данных вызывает малое изменение решения (т.е. решение устойчиво).

Лит.: Бицадзе А. В. Уравнения математической физики. 2-е изд. М., 1982; Владимиров В. С. Уравнения математической физики. 5-е изд. М., 1988; Тихонов А. Н., Самарский А. А. Уравнения математической физики. 7-е изд. М., 2004.