Ланжевена-Дебая формула

ЛАНЖЕВЕНА-ДЕБАЯ ФОРМУЛА, соотношение, связывающее диэлектрическую проницаемость ε полярного диэлектрика с электрическими характеристиками составляющих его молекул. Получена П. Дебаем в 1912 году. Ланжевена-Дебая формула имеет вид:

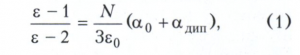
где N - число молекул в единице объёма диэлектрика; ε₀ - электрическая постоянная; α₀ - поляризуемость отдельных молекул (α₀ = р/Е_лок, где Е_лок - напряжённость локального электрического поля, действующего на молекулы, р - дипольный момент молекул, возникающий вследствие их деформации в электрическом поле); в общем случае α₀ = α_эл + α_ион, где α_эл - электронная поляризуемость, вызванная смещением электронной оболочки атома относительно ядра под действием поля, α_ион - ионная поляризуемость, обусловленная смещением ионов по отношению к другим ионам, α_дип - дипольная (ориентационная) поляризуемость, возникающая, если молекулы диэлектрика имеют постоянный дипольный момент р₀ в отсутствие внешнего электрического поля и могут под действием локального электрического поля свободно изменять свою пространственную ориентацию. Если диэлектрик состоит из молекул различных сортов, то N(α₀ + α_дип) заменяется на ∑_i N_i (α_0i + α_{дип i}), где суммирование производится по всем сортам молекул.

П. Дебай получил для дипольной поляризуемости выражение:

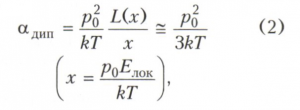
где k - постоянная Больцмана, Т - абсолютная температура, L(х) = cth x – 1/x - функция, введённая П. Ланжевеном (1905) для расчёта намагниченности парамагнитных газов. Приближённое равенство в выражении (2) выполняется с относительной погрешностью, не превышающей р₀Е_ЛОК/(15kТ).

Подстановка приближения (2) в (1) с учётом равенства N = N_Aр/М приводит Ланжевена-Дебая формулу для диэлектрика, состоящего из молекул одного сорта, к виду:

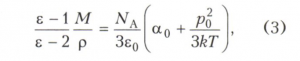
где М - мольная масса, р - плотность диэлектрика, N_A - постоянная Авогадро. Измерения температурной зависимости левой части формулы (3) позволяют определить р₀ и α₀ отдельной молекулы диэлектрика.

Ланжевена-Дебая формула выполняется и для диэлектриков, находящихся в переменном электрическом поле, так как дипольные моменты молекул ещё успевают ориентироваться вслед за полем вплоть до СВЧ-диапазона. В более высокочастотных микроволновом и ИК-диапазонах α_дип = 0 (как и для неполярных диэлектриков с р₀ = О) и Ланжевена-Дебая формула переходит в Клаузиуса - Моссотти формулу, а в видимом и УФ- диапазонах (когда уже и ионы не успевают смещаться вслед за полем и α_ион  = 0) переходит в Лоренца - Лоренца формулу.

При выводе Ланжевена-Дебая формулы предполагается, что молекулы находятся в локальном поле, описываемом формулой Лоренца: Е_лок = Е_ср + Р/(3ε₀), где Е_ср - средняя напряжённость электрического поля в диэлектрике, Р - вектор поляризации диэлектрика. Это справедливо для изотропных диэлектриков (газы и пары при низких давлениях или слабые растворы полярных диэлектриков в неполярных растворителях, для которых и применима Ланжевена-Дебая формула), а также для твёрдых диэлектриков с кубической кристаллической структурой, для которых применимы предельные случаи Ланжевена-Дебая формулы: формула Клаузиса - Моссотти или формула Лоренца - Лоренца.

Лит.: Киттель Ч. Введение в физику твердого тела. М., 1978.