Вариация функции

ВАРИАЦИЯ ФУНКЦИИ, характеристика колебаний функции. Для функции f(х), заданной на отрезке [а, b], вариацией называется точная верхняя грань сумм

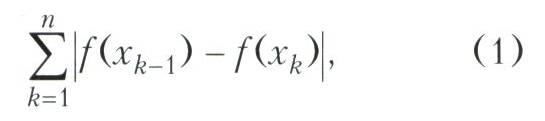
взятая по всевозможным разбиениям отрезка [а, b] точками а = х₀<х₁< ...<х_n = b. Значение этой верхней грани, если оно конечно, называют вариацией функции f на |а, b|. В этом случае функцию f называют функцией ограниченной вариации или функцией с конечным изменением. Множество таких функций обычно обозначают V.

Если производная функции f непрерывна на [а, b], то fЄV и вариация f равна _b∫^a|f ‘(x)|dx. Функция f принадлежит V в том и только том случае, когда её можно представить в виде разности двух возрастающих ограниченных функций. Функции из V непрерывны всюду, за исключением не более чем счётного множества точек, в которых они имеют разрывы первого рода, и почти всюду имеют производную.

Функции ограниченной вариации введены М. Э. К. Жорданом (1881) в связи с изучением сходимости тригонометрических Фурье рядов. Он доказал, что ряды Фурье для функций f из V сходятся в каждой точке.

Функции ограниченной вариации нашли широкое применение во многих разделах математики, в частности в теории интеграла Стилтьеса.

Рассматривают обобщения вариации функций, когда вместо верхней грани сумм (1) берутся верхние грани сумм

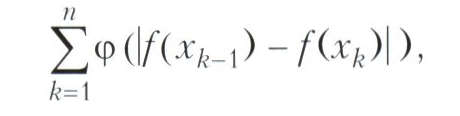
где  φ(t) - возрастающая непрерывная положительная при t > 0 функция и  φ(0) = 0, например,  φ(t) = t^р, р> 1.

Известно несколько различных определений вариации функций многих переменных.

Лит.: Витушкин А. Г. О многомерных вариациях. М., 1955; Натансон И. П. Теория функций вещественной переменной. СПб., 1999.