Векторное пространство

ВЕКТОРНОЕ ПРОСТРАНСТВО (линейное пространство), одно из фундаментальных понятий алгебры, обобщающее понятие совокупности (свободных) векторов. В векторном пространстве вместо векторов рассматриваются любые объекты, которые можно складывать и умножать на числа; при этом требуется, чтобы основные алгебраические свойства этих операций были такими же, как и для векторов в элементарной геометрии. В точном определении числа заменяются элементами любого поля К. Векторным пространством над полем К называется множество V с операцией сложения элементов из V и операцией умножения элементов из V на элементы из поля К, которые обладают следующими свойствами:

х + у = у + х для любых х, у из V, т. е. относительно сложения V является абелевой группой;

λ(х + у) = λ χ + λу для любых λ из К и х, у из V;

(λ +  μ)х = λх +  μх для любых λ,  μ из К и х из V;

(λ μ)х = λ( μх) для любых λ,  μ из К и х из V;

1х = х для любого х из V, здесь 1 означает единицу поля К.

Примерами векторного пространства являются: множества L¹, L² и L³ всех векторов из элементарной геометрии, соответственно на прямой, плоскости и в пространстве с обычными операциями сложения векторов и умножения на число; координатное векторному пространству Kⁿ, элементами которого являются всевозможные строки (векторы) длины n с элементами из поля К, а операции заданы формулами

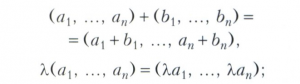
множество F(M, К) всех функций, оп­ределённых на фиксированном множе­стве М и принимающих значения в поле К, с обычными операциями над функ­циями:

Элементы векторного пространства е₁ ..., е_n называются линейно независимыми, если из равенства λ₁e₁ + ... +λ_nе_n = 0 Є V следует, что все λ₁, λ₂,..., λ_n = 0 Є К. В противном слу­чае элементы е₁, е₂, ···> е_n называются линейно зависимыми. Если в векторном пространстве V любые n + 1 элементов e₁,..., е_n+1 ли­нейно зависимы и существует n линей­но независимых элементов, то V назы­вается n-мерным векторным пространством, а n - размерно­стью векторного пространства V. Если в векторном пространстве V для любого натурального n существует n линейно независимых векторов, то V называется бесконечномерным векторным пространством. Например, векторное пространство L¹, L², L³ и Кⁿ соответственно 1-, 2-, 3- и n-мерны; если М - бесконечное множество, то векторное пространство F(М, К) бесконечномерно.

Векторное пространство V и U над полем К называются изоморфными, если существует взаимно однозначное отображение  φ : V -> U такое, что  φ(х+у) =  φ(х) +  φ(у) для любых х, у из V и  φ(λх) = λ φ(х) для любых λ из К и х из V. Изоморфные векторные пространства являются алгебраически неразличимыми. Классификация конечномерных векторных пространств с точностью до изоморфности даётся их размерностью: любое n-мерное векторное пространство над полем К изоморфно координатному векторному пространству Кⁿ. Смотри также Гильбертово пространство, Линейная алгебра.

В. Л. Попов.