Веса (в статистике)

ВЕСА в статистике, коэффициенты, используемые для вычисления среднего значения (средневзвешенного) элемента в совокупности; сумма коэффициентов равна единице. Взвешивание - фундаментальный методический приём, предназначенный для корректного сопоставления количественных значений показателей с учётом их качественной значимости.

Например, если в спортивной команде 10 человек имеют возраст 20 лет, а 1 человек - 30 лет, то средний возраст этой команды составит:

20 лет·(10/11) + 30 лет·(1/11) =  20,9 года.

В этом случае весами выступают значения долей, которые имеют группы соответствующего возраста в общем количестве людей, для которого рассчитывается средний возраст.

Если известны цены  Р₁(t), P_i(t), P_n(t) на товары и услуги в году t и аналогичные показатели для года t + 1, для каждого товара индекс цены за период от года t до года t + 1 можно рассчитать как IP_i(t+ 1/t) =P_i(t+ 1)/Р_i(t). Однако интерес представляет оценка индекса цен в целом, т. е. совокупное изменение цен по всем товарам. Например, для ответа на вопрос о росте стоимости жизни ключевое значение имеет обобщающий, средний индекс цен на потребительские товары и услуги - индекс потребительских цен. При этом нельзя просто использовать среднее арифметическое индексов по отдельным товарам (услугам), поскольку вклад каждого из них в общий рост цен не одинаков, а пропорционален объёму продаж данного товара (услуги). В этой связи каждому индексу цены отдельного товара (услуги) приписывается удельный вес k_i, измеряемый в долях единицы и отражающий долю каждого товара (услуги) в общем росте цен. В итоге общий индекс цен IP(t+1/t) рассчитывается как средневзвешенное:

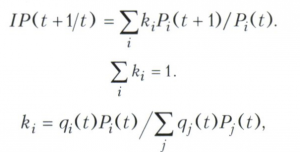
где q_i(t) - количество товара в натуральном исчислении в году t.

При расчёте индекса в качестве весов можно использовать структуру продаж первого (t) или второго (t+ 1) из сопоставляемых периодов. Поскольку эти две структуры могут различаться, то результат расчёта зависит от того, структура какого периода используется для взвешивания. Если взвешивание опирается на структуру первого (базового) периода, как в приведённом примере, то такой индекс называется индексом Ласпейреса, если на структуру второго периода - то индексом Пааше.

А. Е. Косарев.