Винеровский процесс

ВИНЕРОВСКИЙ ПРОЦЕСС, случайный процесс, служащий математической моделью броуновского движения. Винеровский процесс определяется как случайный процесс X(t) с непрерывным временем t Є Т (обычно Т= [0,∞) или Т = [0, 1]) с Х(0) = 0, приращения которого за непересекающиеся промежутки времени взаимно независимы, при этом Х(s + t) - Х(s) при любом s имеет нормальное распределение с нулевым математическим ожиданием и дисперсией t. Такой Винеровский процесс называется стандартным. Произвольный Винеровский процесс, у которого приращения за время t распределены с математическим ожиданием θf и дисперсией σ²t, линейно преобразуется к стандартному Винеровскому процессу; θ и σ² называются соответственно коэффициентами сноса и диффузии. Винеровский процесс в терминах общей классификации случайных процессов является однородным марковским процессом с непрерывным временем и непрерывным пространством состояний. Плотность р(t; х, у) переходной вероятности Винеровского процесса (характеризующая переход из х в у за время t) представляет собой единственное решение уравнения диффузии

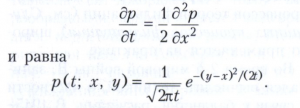
Для любых n и 0 < t₁ < ... < t_n< Т совместное распределение случайных величин Х(t₁), ..., Х(t_n) нормально.

Первая строгая теория процесса броуновского движения была дана Н. Винером (1918-23).

Лит.: Леви П. Стохастические процессы и броуновское движение. М., 1972; Прохоров Ю.В., Розанов Ю.А. Теория вероятностей. 3-е изд. М., 1987.