Вириала теорема

ВИРИАЛА ТЕОРЕМА (немецкий Virial, от латинского vires, множественное число от vis - сила), соотношение, связывающее среднюю кинетическую энергию классической системы N частиц (с массами m_i, координатами r_i и скоростями v_i) с действующими в ней силами F_i . Понятие вириала С = ∑ r_iF_i; введено Р. Ю. Э. Клаузиусом. Им же в 1870 году доказана Вириала теорема, согласно которой  2K(v) = -С, где Κ(ν) = ∑m_iv_i² /2 - кинетическая энергия, а черта сверху означает усреднение по бесконечно большому промежутку времени. Если силы F_i характеризуются потенциалом U_i, то Вириала теорема принимает вид:

В такой форме Вириала теорема справедлива также и для квантово-механических систем, если черту сверху понимать как квантово-механическое среднее, а стоящие под ней выражения - как соответствующие этим величинам квантово-механические операторы.

В статистической механике усреднение по времени заменяется на усреднение по каноническому распределению Гиббса. При этом средняя кинетическая энергия К(v) оказывается равной 3NkT/2 (Т - абсолютная температура, k - постоянная Больцмана). Средний вириал внешних сил, обеспечивающих нахождение системы N частиц внутри сосуда с объёмом V и поддерживающих в нём давление р, равен 3pV. Для этой системы Вириала теорему можно записать в виде вириального уравнения состояния:

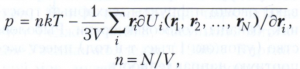
где U_i - энергия взаимодействия i-той частицы с остальными. Это уравнение может служить исходным при получении уравнения состояния неидеального классического газа, в частности вириального разложения для него.

Если потенциальная энергия является однородной функцией n-го порядка, т. е. U(r)~rⁿ, то средняя кинетическая и средняя потенциальная энергии связаны простым соотношением: К(v) = nU(r)/2. В частности, для гармонического осциллятора (n = 2) К = U, для кулоновского и гравитационного потенциалов (n = -1) К = -U/2.

Вириала теорема находит применение в статистической физике, астрофизике, теории атомных систем.

Лит.: Кубо Р. Статистическая механика. М., 1967; Зубарев Д.Н. Неравновесная статистическая термодинамика. М., 1971.