Вращательное движение

ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ твёрдого тела,

1) вращательное  движение вокруг неподвижной оси - движение тела, при котором какие-либо две его точки остаются неподвижными во всё время движения. Прямая, соединяющая эти две точки (и также остающаяся неподвижной), называется осью вращения. При таком движении все точки тела, не лежащие на оси, описывают окружности, лежащие в плоскостях, перпендикулярных оси вращения, с центрами, находящимися на этой оси. Положение тела в пространстве определяется величиной угла поворота φ - двугранного угла, образованного неподвижной полуплоскостью, проходящей через ось вращения, и полуплоскостью, неизменно связанной с вращающимся телом и также проходящей через ось вращения (рис.).

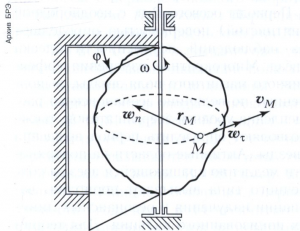Зависимость угла φ от времени φ = φ(t) выражает закон вращательного движения твёрдого тела. Производная dφ/dt = ω(t) называется угловой скоростью вращения тела, а производная da/dt = ε(t) угловым ускорением. Угловую скорость тела можно изобразить в виде вектора ω = ωk, где k - единичный вектор оси вращения. Тогда вектор скорости v_M произвольной точки М тела можно представить в виде векторного произведения:

v_M = ω x r_M,

где  r_M - радиус-вектор точки М в неподвижной системе координат.

Величина скорости ν_Μ = ωr, где r - радиус окружности, по которой движется точка М. Вектор ускорения ν_Μ точки М вращающегося тела представляется в виде суммы w^τ_M и нормального wⁿ_M ускорений: w_M = w^τ_Μ + + wⁿ_M. Величины этих ускорений соответственно равны w^τ_M = er, wⁿ_M = ω²r.

2) вращательное движение вокруг неподвижной точки - движение тела, при котором одна из его точек остаётся неподвижной, а все другие точки тела могут двигаться лишь по сферам с общим центром в неподвижной точке. При таком вращательном движении тела в каждый момент времени скорости его точек оказываются такими, как если бы тело совершало вращательное движение вокруг некоторой оси. Это означает, что существуют такие точки тела, скорости которых в данный момент времени равны нулю. Эти точки образуют мгновенную ось вращения тела, вдоль которой направлен вектор угловой скорости ω. С течением времени эта ось непрерывно изменяет своё положение. При этом скорость любой точки М тела определяется по формуле (1).

В. М. Морозов.