Звёздная статистика

ЗВЁЗДНАЯ СТАТИСТИКА, раздел звёздной астрономии, в котором исследуются взаимосвязи между различными физическими характеристиками звёзд и звёздных скоплений, а также строение, звёздные населения и подсистемы Галактики на основе массовых наблюдательных данных.

Изучение строения нашей Галактики и Вселенной в целом базируется на умении определять расстояния до объектов различной природы: звёзд, звёздных скоплений, газовых туманностей и галактик. Поэтому одной из наиболее важных задач звёздной статистики является установление шкалы расстояний. Поскольку определение надёжных расстояний прямыми геометрическими методами (тригонометрический параллакс) возможно лишь для ограниченного числа относительно близких звёзд и звёздных скоплений (не далее 100-200 пк от Солнца), расстояния до более далёких объектов определяются косвенными методами. В их основе лежит принцип «стандартной свечи», то есть сравнение видимой звёздной величины m звезды с известной абсолютной звёздной величиной М, которые связаны простым соотношением: m - М = 5lgr(пк) - 5 + Е(r), где Е(r) - межзвёздное поглощение света на пути до звезды, r - расстояние вдоль луча зрения.

«Стандартными свечами» могут служить звёзды любого спектрального класса и класса светимости, но в первую очередь это легко отождествляемые и яркие объекты, например некоторые типы переменных звёзд (цефеиды, сверхновые типа Ia и др.). У цефеид существует зависимость между средней абсолютной звёздной величиной (М) и периодом Р пульсаций: (М) = а + blgP. С её помощью удаётся определять расстояния до далёких галактик вплоть до расстояний 20 Мпк. Сверхновые звёзды типа Ia в максимуме блеска - одни из ярчайших объектов во Вселенной - широко используются в космологии для определения самых больших расстояний. Взаимная калибровка светимостей «стандартных свечей» различных типов проводится по звёздным скоплениям или галактикам, содержащим как те, так и другие объекты. Особым классом «стандартных свечей» служат рассеянные и шаровые звёздные скопления, расстояния до которых определяются путём сравнения видимых и абсолютных величин звёзд главной последовательности. Эти расстояния известны с большой точностью, так как для их определения используется большое число звёзд. Светимость «стандартных свечей» - пример важнейших калибровочных связей звёздных характеристик, встречающихся в звёздной астрономии.

Большое значение в звёздной астрономии и астрофизике имеют статистические связи (калибровки) между наблюдаемыми и вычисляемыми физическими характеристиками звёзд, устанавливаемые, как правило, по звёздам с хорошо известными расстояниями и звёздным скоплениям. С помощью калибровок удаётся по наблюдаемым параметрам определить ряд характеристик, недоступных прямым измерениям. Это калибровочные соотношения между нормальным цветом, с одной стороны, и эффективной температурой, болометрической поправкой и абсолютной звёздной величиной - с другой. Существуют также статистические связи между вычисленными величинами (например, зависимость масса - светимость для звёзд главной последовательности) и между наблюдаемыми характеристиками (спектральный класс - нормальный цвет, ультрафиолетовый избыток цвета - содержание тяжёлых химических элементов и др.). Большинство соотношений являются многомерными, поскольку отражают зависимость не только от параметров звёзд, но и от их эволюционного статуса, т. е. класса светимости. Примером двумерной функции распределения по абсолютным звёздным величинам и нормальным цветам служит Герцшпрунга-Рессела диаграмма (цвет - абсолютная звёздная величина) с семью основными последовательностями (классами светимости) звёзд на ней, от сверхгигантов до белых карликов. Диаграмма Герцшпрунга-Рессела представляет собой эффективный инструмент описания звёздных населений и исследования проявлений звёздной эволюции, широко применяемый в звёздной астрономии и астрофизике.

Математический аппарат звёздной статистики - использование статистических функций распределения (в том числе многомерных) объектов по различным характеристикам. В звёздной статистике используются распределения звёзд по абсолютным звёздным величинам (так называемая функция светимости) и по видимым звёздным величинам (так называемая дифференциальная функция блеска). Распределение звёзд в телесном угле вдоль луча зрения по расстояниям представляет собой распределение плотности, тесно связанное с общим распределением массы в Галактике. Из-за влияния эффектов селекции функция светимости наиболее надёжно определяется по звёздам вблизи окрестностей Солнца, а также звёздам - членам рассеянных звёздных скоплений. Из функции светимости выводится функция масс - распределение звёзд главной последовательности по массам, широко применяемая в астрофизике. Важной проблемой остаётся поведение функции светимости слабых (маломассивных) звёзд, которые могут внести большой вклад в полную массу Галактики.

Для исследования строения звёздных подсистем и населений Галактики используется метод звёздных подсчётов, впервые применённый У. Гершелем ещё в 18 веке. В начале 20 века К. Шварцшильд вывел интегральное уравнение, связывающее непосредственный результат звёздных подсчётов - дифференциальную функцию блеска А(m), закон распределения звёздной плотности вдоль луча зрения D(r), функцию светимости Ф(М) и величину межзвёздного поглощения света Е(r):

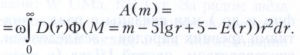
Здесь ω - телесный угол наблюдений. В современной астрономии используют многоцветные дифференциальные функции блеска, полученные при наблюдениях в разных направлениях в Галактике, и многоцветные функции светимости, а вместо прямого решения интегрального уравнения применяют метод популяционного синтеза. Он состоит в том, что Галактика представляется совокупностью взаимопроникающих подсистем, каждая из которых характеризуется определённым законом пространственного распределения, звёздным населением, возрастом, химическим составом, происхождением, начальной функцией масс. В результате звёздная плотность D(r) становится функцией множества параметров (не только структурных, но и астрофизических) и решается задача их оптимального подбора, при котором модельные функции блеска лучше всего согласуются с наблюдаемыми функциями А(m). Для строгого решения требуется знать ход поглощения Е(r) с расстоянием в разных направлениях, т. е. трёхмерную модель распределения поглощающей материи. На больших расстояниях от плоскости симметрии Галактики ход поглощения с расстоянием неплохо описывается моделью плоских слоёв с экспоненциальным уменьшением плотности пыли. Отсутствие адекватных моделей поглощения вблизи плоскости Галактики пока не даёт возможности построения надёжных моделей распределения звёзд в наиболее плотных частях галактического диска, хотя большие надежды связываются с наблюдениями в ИК-диапазоне.

В современных подходах к популяционному моделированию Галактики учитывается её многокомпонентное строение, включающее не менее трёх главных структурных компонентов: диск (тонкий и толстый), балдж (яркая центральная популяция звёзд), галактическая корона (внутренняя и внешнее гало). Они различаются размерами и законами изменения пространственной плотности. Радиальное и вертикальное распределения звёзд в тонком и толстом диске описываются экспоненциальными законами, в то время как для балджа и сфероида используются более сложные степенные или нормальные распределения, часто с учётом трёхосности балджа и наличия центрального бара (перемычки). Наиболее сложно строение тонкого диска, состоящего из целого ряда взаимопроникающих подсистем, различающихся возрастом (от миллионов лет до 8-10 миллиардов лет), характерной толщиной (от 100 до 400 пк) и кинематическими характеристиками. Радиус видимого диска Галактики составляет примерно 20-25 кпк, полная масса Галактики в этих пределах близка к 200 миллиардам масс Солнца. Для описания тёмной материи в модель распределения масс часто вводится почти сферическая «корона» с изотермическим распределением плотности. Одной из важнейших структурных и динамических характеристик Галактики является звёздная плотность вблизи Солнца. По данным о ближайших звёздах, она близка к 0,12 + 0,02 звезды на кубический парсек. Плотность массы при этом (с учётом вклада межзвёздного вещества) оценивается в 0,075 ±0,01 массы Солнца на кубический парсек.

Лит. смотри при ст. Звёздная астрономия.

А. С. Расторгуев.