Аналитическая Функция

АНАЛИТИЧЕСКАЯ ФУНКЦИЯ, функция, которая может быть представлена степенными рядами. Исключительная важность класса аналитической функции определяется следующим. Во-первых, этот класс достаточно широк: он охватывает большинство функций, встречающихся в основном разделах математики и её приложениях в естествознании и технике. Аналитическими являются элементарные функции многочлены, рациональные функции, показательные и логарифмические, степенные, тригонометрические и обратные тригонометрические, гиперболические и обратные гиперболические функции, а также алгебраические функции и специальные функции (эллиптические, цилиндрические и др.). Во-вторых, класс аналитической функции замкнут относительно основных операций арифметики, алгебры и анализа: применение арифметических действий к функциям этого класса, решение алгебраических уравнений с аналитическими коэффициентами, дифференцирование и интегрирование аналитической функции снова приводят к аналитической функции. Наконец, аналитические функции обладают свойством единственности: каждая аналитическая функция образует «органически связанное целое», представляет собой «единую» функцию во всей своей естественной области существования. Это свойство, которое в 19 веке считалось неотделимым от самого понятия функции, приобрело принципиальное значение после того, как в 19 веке установилась общая точка зрения на функцию как на произвольное соответствие.

Теория аналитической функции создана в 19 веке, в первую очередь благодаря работам О. Коши, Б. Римана и К. Вейерштрасса. Решающую роль в построении этой теории сыграл переход от действительного переменного х к комплексному переменному z = х + iy, лежащему в комплексной плоскости. Теория аналитической функции  возникла как теория функций комплексного переменного; в некотором смысле именно аналитические функции  (а не произвольные комплексные функции двух действительных переменных х и у) естественно считать функциями комплексного переменного z. Поэтому часто под теорией функций комплексного переменного понимают именно теорию аналитической функции.

Существуют различные подходы к понятию аналитичности. В основе одного из них, предложенного О. Коши и развитого Б. Риманом, лежит структурное свойство функции - существование производной по комплексному переменному (комплексная дифференцируемость). Этот подход тесно связан с геометрическими соображениями. Другой подход, развивавшийся К. Вейерштрассом, основывается на возможности представления функций степенными рядами; он связан тем самым с аналитическим аппаратом, с помощью которого может быть представлена функция. Основной факт теории аналитической функции  заключается в тождественности соответствующих классов функций, рассматриваемых в произвольной области комплексной плоскости.

Приведём точные определения. Геометрически число z = х + iy изображается точкой плоскости с координатами х и у; евклидова плоскость, точки которой отождествляются с комплексными числами, называется комплексной плоскостью. Пусть D - область (открытое связное множество) в комплексной плоскости. Если каждой точке z области D поставлено в соответствие некоторое комплексное число w, то говорят, что в области D определена (однозначная) функция f комплексного переменного z, и пишут w = f(z), zЄD. Функция w =  f(z) = f(х + iy) комплексного переменного z Є D может рассматриваться как комплексная функция двух действительных переменных х и у, определённая в области D. Если f дифференцируема в точке z Є D как функция (х, у), то в этой точке определены (формальные) производные

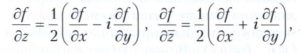
а приращение Δf(z) = f(z+Δz) - f(z) представляется в виде

где zz = х-iy, o(Δz)/Δz→0 при Δz→0. Если (df/dzz)(z) = 0, то существует предел f’(z) отношения Af(z)/Δz при Δz→0, который называется производной функции f в точке z, а f называется комплексно дифференцируемой в этой точке. Если это свойство имеет место для любой точки z области D, то функция f называется комплексно дифференцируемой (или голоморфной) в D. Таким образом, голоморфность f в D означает дифференцируемость f в D по переменным х, у и выполнение условий Коши-Римана (df/dzz)(z) = 0, которые в терминах действительных переменных х,у и функций u, v, f=u+iv, называемых действительной и мнимой частью функции f, записываются в виде системы уравнений Коши-Римана:

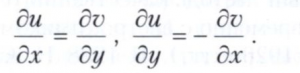
Равенство (df/dz)(z) = 0 показывает, что комплексно дифференцируемыми являются те и только те функции f, которые, рассматриваемые формально как функции независимых переменных z и zz?, зависят только от z.

Функция f, определённая в области D, называется аналитической в точке z₀ Є D, если существует окрестность этой точки, в которой f представляется степенным рядом

Если это свойство имеет место в каждой точке z₀ Є D области D, то функция f называется аналитической в D.

В теории функций комплексного переменного доказывается, что всякая функция f, комплексно дифференцируемая (голоморфная) в области D, аналитична в этой области. С другой стороны, функция f, аналитическая в точке z₀ области D, комплексно дифференцируема в этой точке (и даже бесконечно дифференцируема по комплексному переменному z). Следовательно, понятия комплексной дифференцируемости и аналитичности функции в области тождественны.

Если Е - произвольное множество в комплексной плоскости, то функция f(z), z Є Е, называется аналитической (голоморфной) на Е, если существует открытое множество, содержащее Е, и аналитическая на нём функция f, совпадающая с f на множестве Е. Для открытых множеств понятие аналитичности эквивалентно понятию комплексной дифференцируемости на множестве, однако в общем случае это не так.

Важнейшее свойство аналитической функции  выражается следующей теоремой единственности: две функции, аналитические в области D и совпадающие на каком-либо множестве, имеющем предельную точку в D, совпадают и во всей области D. В частности, аналитическая функция, отличная от тождественного нуля, может иметь в области лишь изолированные нули.

Важную роль в изучении аналитической функции  играют точки, в которых нарушается свойство аналитичности, - так называемые особые точки аналитической функции.  Функция f, аналитическая в области вида 0<|z - z₀|<р, разлагается в ней в ряд Лорана

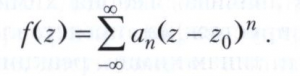
Если в этом разложении члены с отрицательными степенями отсутствуют

и точка z₀ называется правильной точкой f. Если ряд Лорана функции f содержит лишь конечное число членов с отрицательными степенями z-z₀, то точка z₀ называется полюсом функции f: в этом случае          

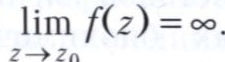
Если же ряд Лорана функции f содержит бесконечное число отрицательных степеней z-z₀, то z₀ называется существенно особой точкой; в таких точках не существует ни конечного, ни бесконечного предела функции f.

Функции, представимые в виде отношения двух функций, аналитических в области D, называются мероморфными в D. Мероморфная в области функция аналитична в ней за исключением конечного или счётного множества полюсов; в полюсах значения мероморфной функции считаются равными бесконечности.

Простейший класс аналитической функции  составляют функции, аналитические во всей комплексной плоскости; такие функции называются целыми. К ним относятся, например, многочлены от z, функции е², sin z, cos z. Функции, мероморфные во всей плоскости, - это, например, рациональные функции от z (отношения многочленов), tg z = sin z/cos z, ctg z = cos z/sin z, эллиптические функции.

Для изучения аналитической функции  важное значение имеют связанные с ними геометрические представления. Функцию w = f(z), zЄD, можно рассматривать как отображение области D в комплексную плоскость переменной w. Если f есть аналитическая функция, то образ f(D) области D также является областью (принцип сохранения области). Если f’(z₀) ≠ 0, то соответствующее отображение сохраняет углы в точке z₀ как по абсолютному значению, так и по знаку, т. е. является конформным.

Действительная и мнимая части u и v аналитической функции  f в области D удовлетворяют в ней уравнению Лапласа

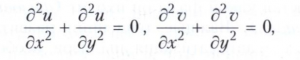
то есть являются гармоническими функциями. Связи с конформными отображениями и гармоническими функциями лежат в основе многих приложений теории аналитической функции.

Всё сказанное выше относилось к однозначным аналитическим функциям  f, рассматриваемым в данной области D. Задаваясь вопросом о возможности продолжения f как аналитической функции  в большую область, приходят к понятию аналитической функции, рассматриваемой во всей своей естественной области существования (смотри аналитическое продолжение). Такая аналитическая функция, вообще говоря, оказывается многозначной, как, например, ⁿ√z, ln z, arcsin z и arctg z, алгебраические функции. К необходимости изучения многозначных аналитических функций  приводят многих вопросы теории функций.

Понятие аналитической функции  нескольких переменных вводится с помощью кратных степенных рядов или условий Коши-Римана, совершенно аналогично тому, как это было сделано выше для аналитической функции  одного переменного. Аналитические функции  нескольких комплексных переменных по своим свойствам во многом аналогичны аналитической функции  одного комплексного переменного, однако они обладают и рядом принципиально новых свойств.

Лит.: Владимиров В. С. Методы теории функций многих комплексных переменных. М., 1964; Голузин Г. М. Геометрическая теория функций комплексного переменного. 2-е изд. М., 1966; Маркушевич А. И. Теория аналитических функций: В 2 т. 2-е изд. М., 1967-1968; Шабат Б. В. Введение в комплексный анализ: В 2 часть 3-е изд. М., 1985; Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. 5-е изд. М., 1987; Евграфов М.А. Аналитические функции. 3-е изд. М., 1991; Привалов И. И. Введение в теорию функций комплексного переменного. 14-е изд. М., 1999.