Асимптотический ряд

АСИМПТОТИЧЕСКИЙ РЯД, ряд

составленный из функций переменной х таких, что при заданном изменении х (например, при х → 0 или при х → ∞) каж­дый следующий член этого ряда есть бесконечно малая величина относитель­но предыдущего члена, т.е. а_n+1(х) = = о(а_n(х)), n = 0, 1, ... (см. Бесконечно большие и бесконечно малые величины).

Такой ряд называется асимптоти­ческим разложением функции а(х) при x→х₀, если для любого n = 0, 1, 2, ...

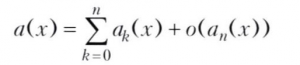
при х→х₀. В этом случае пишут

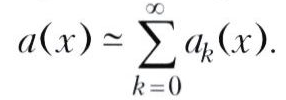
Наряду с символом =?  употребляется также символ ~.

Примером асимптотического разложения является Тейлора формула

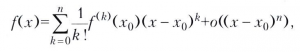
где f⁽⁰⁾(x) = f(x), f^(k)(x) - k-я производ­ная функции f(x), k=1, 2, ..., n, которая даёт степенное асимптотическое разложение

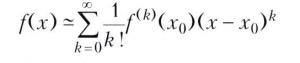
гладкой функции f(x) при х → х₀.

Асимптотический ряд не обязательно сходится. Например, ряд 1-1!х+2!х²-3!х³+... является асимптотическим рядом при x → 0, но расходится при каж­дом х≠0; ряд с общим членом а_n = n!t^-n exр t² является асимптотическим рядом при t → ∞ хотя всюду расходится, а его члены суть бесконечно большие при t → ∞. В отличие от случая сходящихся рядов, где рассматривается абсолютная погрешность приближения, в асимптотических разложениях важна относительная погрешность.

Асимптотические ряды, как и сходящиеся ряды, широко используются как в самой математике, так и в её естественнонаучных приложениях. Частичная сумма ряда обычно даёт удобное приближение исследуемой функции. Асимптотические ряды и разложения часто возникают при наличии в задаче малого или большого параметра.

Отдельные асимптотические разложения использовались в 18 веке. Строгое понятие асимптотического ряда введено А. Пуанкаре (1886) в связи с задачами небесной механики.

Лит.: де Брейн Н.Г. Асимптотические методы в анализе. М., 1961; Эрдейи А. Асимптотические разложения. М., 1962; Федорюк М.В. Метод перевала. М., 1977; Евграфов М. А. Асимптотические оценки и целые функции. 3-е изд. М., 1979; Олвер Ф. Асимптотика и специальные функции. М., 1990; Уиттекер Э. Т.. Ватсон Дж. Н. Курс современного анализа. 3-е изд. М., 2002. Ч. 1.