Боголюбова цепочка уравнений

БОГОЛЮБОВА ЦЕПОЧКА УРАВНЕНИЙ, цепочка уравнений для функций распределения F_s(t, r₁…r_s, р₁,...,p_s) координат и импульсов s частиц в классической статистической системе, состоящей из N частиц, здесь s=1, 2, ..., N-1, t — время, r₁..r_s и р₁..p_s - трёхмерные векторы координат и импульсов частиц. При помощи функций распределения, главным образом F₁ и F₂, могут быть выражены все специфические характеристики статистических систем.

Функции распределения F_s (точнее, плотности распределения) определяются равенствами

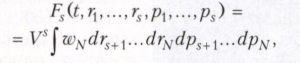
где s=1,2,...,N-1, V - объём системы, w_N - функция распределения (плотность распределения вероятностей) для N частиц, удовлетворяющая уравнению Луинвилля

где H_N – гамильтониан системы из N частиц; фигурные скобки означают скобки Пуассона (смотри ниже). В отличие от w_N функции F_s не нормированы и становятся функциями распределения вероятностей при нормировке величиной V^s.

Боголюбова цепочка уравнений в предельном случае, когда V→∞ V/N=v, где v - положительная постоянная, представляет собой бесконечную систему уравнений, s-е уравнение которой связывает производную dF_s/dt с функцией F_{s + 1}:

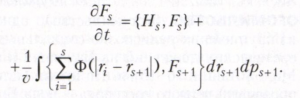
Здесь Ф(|r_i - r_s+1|) - потенциал взаимодействия i-й и (s+ 1)-й частиц, H_s - гамильтониан системы из s частиц (сумма кинетической и потенциальной энергий); фигурные скобки обозначают скобки Пуассона, которые для функций f(t, r₁,..r_s,р₁,..р_s) и g(t,r_1,..r_s,р₁...,p_s) гамильтоновых (канонических) переменных r₁,...r_s, р₁, ...,p_s определяются равенством

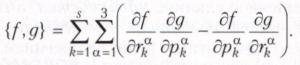
Здесь r^α_k и р^α_k, α=1, 2, 3 - компоненты координат и импульсов частиц, k= 1, ...,s.

Основные трудности исследования Боголюбова цепочки уравнений связаны с проблемами замыкания системы и нахождения решения замкнутой системы со специальными предельными условиями для функций F_s. Эти исследования несколько упрощаются в термодинамически равновесном случае, когда распределение по импульсам каждой частицы является Максвелла распределением, а также в случае короткодействия, когда третья степень эффективного радиуса взаимодействия частиц мала по сравнению с параметром v, и в случае длиннодействия, когда третья степень этого радиуса значительно превосходит v. Боголюбова цепочка уравнений приводит, в частности, к кинетическому уравнению Больцмана для одночастичной функции распределения F₁.

При рассмотрении квантовых статистических систем Боголюбова цепочка уравнений составляется для s-частичных статистических квантовых операторов.

Подход к изучению статистических систем с использованием цепочек уравнений для функций распределения F_s был предложен Н. Н. Боголюбовым (1946), такая цепочка уравнений получила название Боголюбова цепочка уравнений, её также называют ББГКИ-уравнениями, последнее название связано с именами Н. Н. Боголюбова, М. Борна, английских учёных Дж. Грина, Дж. Кирквуда и Дж. Айвона, внёсших существенный вклад в исследования Боголюбова цепочку уравнений.

Боголюбова цепочка уравнений является основным аппаратом изучения классической и квантовой систем в статистической механике.

Лит.: Уленбек Дж., Форд Дж. Лекции по статистической механике. М., 1965; Боголюбов Н.Н. Избранные труды. К., 1970. Т. 2. С.99-196, 227-493; Боголюбов Н.Н., Боголюбов Н.Н. (мл.). Введение в квантовую статистическую механику. М., 1984.