Беллмана уравнение

БЕЛЛМАНА УРАВНЕНИЕ, рекуррентное соотношение для решения задачи оптимального управления с аддитивной целевой функцией. Метод нахождения оптимального управления с помощью Беллмана уравнения получил название динамического программирования. Уравнение носит имя Р. Беллмана, сформулировавшего принципы динамического программирования в конце 1950-х годов.

Решением Беллмана уравнения являются оптимальные значения целевой функции и оптимального управления для всех возможных состояний системы на каждом шаге управления. Нахождение оптимального управления в многошаговой задаче с n шагами начинается с последнего шага, для чего составляется и решается Беллмана уравнение в одношаговой задаче, затем с использованием решения первой задачи составляется и решается Беллмана уравнение с двумя шагами, и так до начального момента, на котором выбирается первый из n шагов.

Например, в задаче распределения ресурсов однородный ресурс Х должен быть распределён между N производственными процессами. Если для k-го процесса выделяется ресурс x_k, то получается доход φ_k(x_k), k= 1, ..., N. Требуется распределить ресурс Х по процессам таким образом, чтобы суммарный доход был максимальным. Другими словами, требуется найти максимум

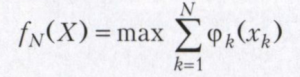
аддитивной целевой функции

при условиях x_k≥0, k=1,…,N; x₁+…x_N=X.

Для применения подхода динамического программирования к данной задаче рассматривается семейство задач с любым числом шагов n≤N и любым запасом ресурса 0≤ х ≤ Х. Многошаговость принятия решения вводится искусственно, на 1-м шаге выделяется ресурс x_n для n-го процесса, на 2-м шаге выделяется ресурс x_n-1 для (n-1)-го процесса и т. д. В силу аддитивности целевой функции справедливо рекуррентное соотношение 

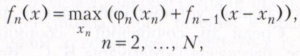
где f₁(x) = φ₁(x). Это рекуррентное соотношение представляет собой Беллмана уравнение в этой задаче. Оно позволяет при всех допустимых значениях х ≤ Х последовательно находить функции f₁(х), ..., f_n(х), начиная с f₁(х), и соответствующие оптимальные управления х₁(х), ..., х_n(х), где x_k(х) - оптимальный выбор ресурса для k-го процесса в задаче с k шагами, k = 1, ..., n.

Оптимальный доход для исходной задачи равен f_N(Х). Тем самым решение исходной задачи максимизация функции от N переменных сводится к решению N задач, в каждой из которых максимизация проводится по одной переменной.

Наряду с задачами с конечным числом шагов рассматриваются задачи с бесконечным числом шагов, а также задачи с непрерывным временем. В задачах оптимального управления с непрерывным временем Беллмана уравнения представляют собой дифференциальные уравнения специального вида.

Лит.: Беллман Р. Динамическое программирование. М., 1960; Беллман Р., Дрейфус С. Прикладные задачи динамического программирования. М., 1965; Флеминг У., Ришел Р. Оптимальное управление детерминированными и стохастическими системами. М., 1978.