Бесконечное произведение
Смотрите также:
БЕСКОНЕЧНОЕ ПРОИЗВЕДЕНИЕ бесконечной последовательности чисел р1, р2, ..., формально записанное произведение
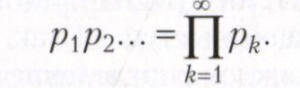
Если последовательность частичных произведений Рn = p1 р2 ... рn при n →∞ сходится к числу Р, не равному нулю, то бесконечное произведение называют сходящимся, Р называют значением бесконечного произведения и пишут Р = ∏∞k=1Рк. Если последовательность Рn не сходится к конечному пределу или сходится к нулю, то бесконечное произведение называют расходящимся.
Сходимость бесконечного произведения, все множители рк которого положительны, равносильна сходимости ряда ∑∞k=1lnpk.
Для сходимости бесконечного произведения необходимо, чтобы рк→1 при k → ∞, поэтому бесконечное произведение часто записывают в виде
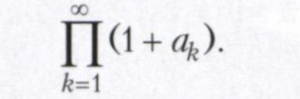
Реклама
Если все числа ak имеют одинаковые знаки, то сходимость такого бесконечного произведения равносильна сходимости ряда ∑∞k=1ak.
Множителями бесконечного произведения могут быть комплексные числа, функции и вообще элементы произвольной природы, для которых определены произведение конечного набора множителей и сходимость последовательностей элементов.
Бесконечные произведения используются для представления многих важных постоянных и функций. Например, Валлиса формула даёт представление числа π в виде бесконечного произведения; установленная Л. Эйлером формула
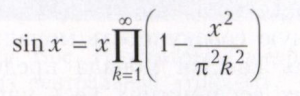
даёт представление функции sin х в виде бесконечного произведения, которое можно рассматривать как аналог разложения многочлена на произведение многочленов первой и второй степеней.
Бесконечные произведения впервые встречаются в работе Ф. Виета (1593).
Лит.: Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. 8-е изд.
М.; СПб., 2003. Т. 2; Ильин В.А., Позняк Э. Г. Основы математического анализа. 5-е изд. М., 2004. Ч. 1.
С. А. Теляковский.