Больцмана распределение

БОЛЬЦМАНА РАСПРЕДЕЛЕНИЕ, статистически равновесная функция распределения f(р, r) по импульсам р и координатам r частиц (атомов, молекул) идеального газа, которые подчиняются классической механике и находятся во внешнем потенциальном поле:

Где р²/2m – кинетическая энергия частицы с  массой m, U(r) - её потенциальная энергия во внешнем поле, Т - абсолютная температура газа, k - постоянная Больцмана. Постоянная А определяется из условия равенства интеграла от f(р,r) по всем р и r полному числу частиц N в системе (условие нормировки). Частным случаем Больцмана распределения при U(r) = 0 является Максвелла распределение частиц по скоростям.

Больцмана распределение может быть получено из Гиббса распределения для газа, в котором взаимодействием между частицами можно пренебречь. Поскольку частицы не взаимодействуют между собой, гамильтониан системы можно представить в виде суммы гамильтонианов отдельных частиц и рассматривать распределение не в фазовом пространстве всех частиц, как в статистической механике Гиббса, а в фазовом пространстве координат и импульсов одной частицы.

Функцию распределения ( 1 ) иногда называют распределением Максвелла - Больцмана, а распределением Больцмана - функцию распределения (1), проинтегрированную по всем импульсам частиц (она характеризует плотность n числа частиц в точке r):

где n₀ - плотность числа частиц, соответствующая точке, в которой U(r) = 0. Отношение плотностей (n₁ и n₂) числа частиц в различных точках (r₁ и r₂) зависит от разности потенциальных энергий частиц в этих точках:

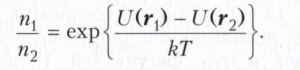
В частном случае отсюда следует барометрическая формула, определяющая распределение плотности числа частиц в поле тяжести над земной поверхностью в зависимости от высоты h. В этом случае U(h) = mgh, где g - ускорение силы тяжести, m — масса частицы.

Для идеальных квантовых газов состояния отдельных частиц определяются не импульсами и координатами, а квантовыми уровнями энергии Е_i частицы в поле U(r). В этом случае Больцмана распределение для средних чисел n_i заполнения i-го квантового состояния имеет вид:

где μ – химический потенциал. Формула (2) есть предельный случай Бозе - Эйнштейна распределения и Ферми - Дирака распределения при таких температурах и плотностях, когда можно пренебречь квантовым вырождением газа, но следует учитывать квантование уровней энергии частиц.

Лит.: Ландау Л. Д., Лифшиц Е.М. Статистическая физика. 3-е изд. М., 1976; Майер Дж., Гепперт Майер М. Статистическая механика. 2-е изд. М., 1980. Гл. 7; Зоммерфельд А. Термодинамика и статистическая физика. М., 2002.