Д’Аламбера-Лагранжа принцип

Д’АЛАМБЕРА-ЛАГРАНЖА ПРИНЦИП, один из основных, наиболее общих дифференциальных вариационных принципов механики, выражающий необходимые и достаточные условия соответствия действительного движения механической системы с идеальными удерживающими связями заданным активным силам. Установлен Ж. Лагранжем в 1788 путём обобщения Д’Аламбера принципа и возможных перемещений принципа.

Согласно Д’Аламбера-Лагранжа принципу, из всех движений системы материальных точек, допускаемых идеальными удерживающими связями в рассматриваемый момент времени и происходящих под действием произвольных активных сил, действительным является то движение, для которого сумма элементарных работ активных сил F_i и сил инерции (-m_iw_i) на любых возможных перемещениях δr_i точек системы равна нулю в любой момент времени:

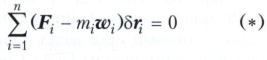
(здесь m_i - масса материальной точки, w_i - её ускорение, n - число точек системы).

Уравнение (*) представляет собой общее уравнение механики систем с идеальными удерживающими связями. Оно справедливо и для связей с трением, если в число задаваемых сил формально включить силы трения точек системы о связи. Можно сказать, что вся динамика систем материальных точек сводится к одному общему уравнению (*). Если все w_i = 0, то уравнение (*) является общим уравнением статики.

Из уравнения (*) можно получить как следствия общие теоремы динамики (об изменении количества движения, об изменении момента количества движения системы, об изменении кинетической энергии), уравнения движения механических систем в различных системах координат и при различных предположениях относительно сил и связей (уравнения Лагранжа, Аппеля и др.).

Д’Аламбера-Лагранжа принцип  справедлив как для голономных, так и для неголономных систем. Все другие вариационные принципы механики представляют собой иные формулировки этого принципа или следствия из него.

В. М. Морозов.