Динамическое программирование
ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ, раздел оптимального управления, посвящённый теории и методам решения многошаговых задач. В задачах оптимального управления среди возможных управлений ищется то, при котором достигается экстремальное (наименьшее или наибольшее) значение так называемой целевой функции - некоторой числовой характеристики процесса. В динамическом программировании под многошаговостью понимают либо многоступенчатую структуру процесса, либо то, что управление разбивается на ряд последовательных этапов (шагов), соответствующих, как правило, различным моментам времени. Иногда многошаговость проистекает из существа процесса, но она может вводиться и искусственно для того, чтобы обеспечить возможность применения методов динамического программирования. Под программированием в динамическом программировании понимают принятие решений (планирование), а слово «динамическое» указывает на существенную роль времени и порядка выполнения операций. Методы динамического программирования являются составной частью методов, используемых в исследовании операций, и применяются в задачах оптимального планирования (например, в задачах об оптимальном распределении ресурсов, в теории управления запасами, в задачах замены оборудования) и при решении многих технических проблем (например, в задачах управления последовательными химическими процессами, в задачах оптимальной прокладки дорог).
Реклама
Пусть процесс управления некоторой системой Х состоит из m шагов (этапов); на i-м шаге управление yi переводит систему из состояния xi-1, в котором она находилась после (i - 1)-го шага, в новое состояние xi. При этом задана функция fi(х, у), и новое состояние определяется по этой функции значениями xi-1, yi так, что xi = fi (xi-1, yi), i = 1, 2,..., m. Таким образом, управления у1, у2, ..., уm переводят систему из начального состояния х0 ∈ Х0 в конечное состояние хm ∈ Хm, где Х0 и Хm - совокупности допустимых начальных и конечных состояний системы Х.
Одна из возможных постановок задач динамического программирования состоит в следующем. При заданном начальном состоянии х0 требуется выбрать управления у1, у2, ..., уm таким образом, чтобы система Х перешла в допустимое конечное состояние и при этом заданная целевая функция F(х0, у1, х1,..., уm, хm) достигла максимального значения F*, т. е.
![]()
где максимум берётся по всем управлениям у1, ..., уm, для которых хm ∈ Хm.
В динамическом программировании обычно предполагается, что целевая функция является аддитивной. В рассмотренном примере это означает, что
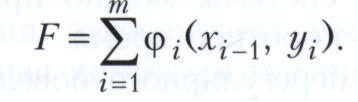
Кроме того, в динамическом программировании предполагается, что в задаче отсутствует последействие: решения (управления), принимаемые на шаге i, оказывают влияние только на состояние xi системы в момент i. Оба упомянутых ограничительных условия можно ослабить, но только за счёт существенного усложнения метода.
В основе динамического программирования лежит принцип оптимальности, сформулированный Р. Беллманом. Пусть выбраны некоторые управления у1, у2, ..., yk и тем самым траектория х0, х1 , ...,xk состояний и требуется завершить процесс, т. е. выбрать у k+1, ..., уm ( а значит, и xk+1, ..., хm).
Если завершающая часть процесса не будет оптимальной в смысле достижения максимума функции
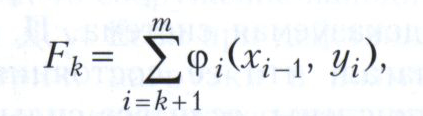
то и весь процесс не будет оптимальным. Пользуясь принципом оптимальности Беллмана, можно получить основное функциональное соотношение динамического программирования, которое состоит в следующем. Пусть ωm(х) = 0,
![]()
k = 1, 2, ..., m, где максимум берётся по всем управлениям у, допустимым на шаге k. Соотношение, определяющее зависимость ωk-1 от ωk, называется уравнением Беллмана. Смысл этих функций достаточно ясен: если система на шаге k-1 оказалась в состоянии х, то ωk-1(х) есть максимально возможное значение функции Fk. Одновременно с построением функций ωk-1(х) находятся условные оптимальные управления yk(х) на каждом шаге, т. е. значения оптимального управления при всевозможных предположениях о состоянии х системы на шаге k-1. Окончательно оптимальные управления находятся последовательным вычислением величин ω0(х0) = F*, у1, х1, у2, ..., уm, xm.
С помощью динамического программирования решается не одна конкретная задача при определённом х0, а сразу все подобные однотипные задачи при любом начальном состоянии. Численная реализация динамического программирования довольно сложна, так как требует запоминания большого количества информации, поэтому динамическое программирование целесообразно применять в тех случаях, когда необходимо многократно решать типовые задачи (например, определение оптимального режима полёта самолёта при меняющихся погодных условиях). Обычно задача динамического программирования формулируется для дискретных процессов, но в ряде случаев динамическое программирование применяется и для решения динамических задач с непрерывными параметрами.
Динамическое программирование дало новый подход ко многим задачам вариационного исчисления. Важный раздел динамического программирования составляют стохастические задачи динамического программирования, т. е. задачи, в которых на состояние системы и на целевую функцию влияют случайные факторы.
Строгое обоснование динамического программирования следует из результатов Л. С. Понтрягина и его учеников по математической теории управляемых процессов.
Лит.: Беллман Р. Динамическое программирование. М., 1960; Математическая теория оптимальных процессов. М., 1961; Ховард Р. А. Динамическое программирование и марковские процессы. М., 1964; Хедли Дж. Нелинейное и динамическое программирование. М., 1967; Хедли Дж., Уайтин Т. Анализ систем управления запасами. М., 1969.