Динамика механизмов и машин

ДИНАМИКА МЕХАНИЗМОВ И МАШИН, раздел теории механизмов и машин, в которой изучается движение механизмов и машин с учётом действующих в них сил. Основные задачи динамики механизмов и машин: изучение законов движения; регулирование движения машин; определение механической кпд механизмов и машин; определение давлений (реакций) в кинематических парах при движении механизма; уравновешивание механизмов и машин. Исследования динамики машин непосредственно связаны с расчётами их элементов на прочность с целью выбора обоснованных размеров и необходимых форм деталей и механизмов.

Определение законов движения основывается на рассмотрении уравнений движения машины или механизма. Число уравнений равно числу степеней свободы. Для механизма с одной степенью свободы уравнение движения может быть представлено в следующей форме:

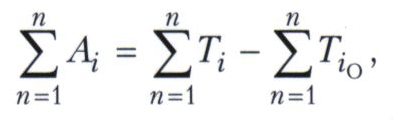
где n - число подвижных звеньев механизма; A_i - работа внешних сил, действующих на звено i за рассматриваемый промежуток времени; T_i и T_i0 - соответственно кинетическая энергия звена i в конце и начале этого промежутка. Соотношение работы движущих сил и сил сопротивления в механизме (машине) определяет характер его движения. Это уравнение можно представить в виде: A_g - А_с = ΔТ, где A_g и А_с соответственно работа движущих сил и сил сопротивления; ΔТ - изменение кинетической энергии механизма за рассматриваемый промежуток времени. При неустановившемся движении абсолютная величина работы движущих сил больше (период разбега) или меньше (на выбеге) абсолютной величины работы сил сопротивления. Равенство работы движущих сил и сил сопротивления в любой момент времени соответствует установившемуся равномерному движению механизма (машины). При установившемся периодическом движении машины алгебраическая сумма работы движущих сил и сил сопротивления равна нулю только за определённый период (цикл) изменения кинетической энергии. Изменение соотношения работы движущих сил и сил сопротивления внутри цикла приводит к колебаниям угловой скорости главного вала машины (биение). Неравномерность вращения оценивается коэффициентом неравномерности вращения δ = (ω_макс - ω_мин)/ω_ср, где ω_ср соответствует номинальной скорости вращения. Допустимый коэффициент δ для каждого типа машины устанавливается на основе результатов опытной эксплуатации.

Определение законов движения звеньев механизма по заданным характеристикам внешних сил решают с помощью дифференциальных уравнений движения механической системы или машинного агрегата, состоящего обычно из двигателя, передаточного механизма, исполнительного и иногда управляющего устройства. Число уравнений равно числу степеней свободы рассматриваемой системы. В плоских механизмах с одной степенью свободы для удобства решения задачи о движении механизма пользуются обычно методом приведения сил или масс, который позволяет заменить задачу о движении всего механизма задачей о движении одного звена (звена приведения), обладающего приведённой массой и находящегося под действием приведённых сил (или моментов). Кинетическая энергия звена при этом равняется сумме кинетических энергий всех звеньев механизма. В результате приведения сил и масс любой   машины  с  одной  степенью  свободы, независимо от её сложности, можно заменить динамический момент на переменный приведённый момент инерции J_п или суммарный приведённый момент движущих сил и сил сопротивления М_п. Уравнение движения звена приведения в реальном механизме:

В общем случае момент М_п зависит от времени, положения звена, скорости. Уравнения движения обычно являются нелинейными, точных методов их решения не существует, поэтому пользуются приближёнными - графическим, графоаналитическим, численным.

Для механизмов с несколькими степенями свободы - в голономных системах (все связи в такой системе являются геометрическими) уравнения движения механизмов составляют обычно в форме уравнений Лагранжа второго рода. Усложняют задачу определения закона движения механической системы необходимость учёта упругости систем и переменности масс звеньев, а также зазоров и трения в кинематических парах.

Задачей регулирования машин и механизмов является получение устойчивого движения, при котором изменение скорости не выходит за допустимые пределы. Для этого рассматривают установившееся периодическое движение машины и рассчитывают уравновешивающуюся массу - маховик. При неустановившемся движении (если возникает необходимость поддерживать среднюю скорость звена приведения на заданном уровне) применяют автоматические регуляторы, влияющие на закон изменения движущих сил либо сил сопротивления.

В задачу определения кпд машин и механизмов входит также исследование потерь в них при работе. Наибольшее значение имеют потери на трение. При установившемся движении величина потерь может быть оценена величиной механического кпд, определяющего степень использования энергии в машине.

При определении давлений (реакций) в кинематических парах проводят кинетостатический расчёт механизмов при заданном законе движения с учётом всех заданных внешних сил, а также сил инерции и сил трения в подвижных соединениях. Значения этих реакций необходимо знать для расчёта звеньев на прочность, подбора подшипников и назначения режимов их смазки.

Задачей уравновешивания механизмов и машин является устранение вредного влияния переменных по величине и направлению сил инерции. Эти силы в современных быстроходных машинах нарушают нормальную работу узлов, являются источником вибрации и шума, оказывают вредное воздействие на окружающую среду и обслуживающий персонал. Для устранения или уменьшения до допустимых  значений  неуравновешенных сил инерции определяют величину и место установки так называемых корректирующих масс, изменяющих положение центра масс рычажного механизма или ротора. Смотри также Машин и механизмов теория.

Историческая справка. Первые расчёты динамических сил в механизмах выполнены в России Н. Е. Жуковским и продолжены Н. И. Мерцаловым; получили развитие начиная с 1930-х годов в трудах И. И. Артоболевского, Н. И. Левитского, А. Ю. Ишлинского, а позднее К. В. Фролова и других учёных в расчётах конкретных машин (например, вибраций в станках, транспортных машинах, переменных сил, действующих при полёте ЛА).

Лит.: Артоболевский И. И. Теория механизмов и машин. М., 1988; Левитский Н. И. Теория механизмов и машин. М., 1990; Теория механизмов и механика машин / Под редакцией К. В. Фролова. М., 2003.