Динамика кристаллической ре­шётки

ДИНАМИКА КРИСТАЛЛИЧЕСКОЙ РЕШЁТКИ, раздел физики твёрдого тела, в котором методами классической и квантовой механики изучаются движения образующих кристалл атомов (ионов, молекул) и связь этих движений с физическими свойствами кристалла. Динамическая теория кристаллической решётки разработана в начале 20 века. В 1907  году А. Эйнштейн с помощью модели кристалла как совокупности квантовых гармонических осцилляторов одинаковой частоты объяснил наблюдаемое уменьшение теплоёмкости твёрдого тела при уменьшении температуры. Более совершенная динамическая теория кристаллической решётки как совокупности квантовых осцилляторов различных частот была построена П. Дебаем (1912), М. Борном и М. Лауэ (1913-15).

Движения атомов в кристалле обычно представляют собой малые колебания атомов около своих положений равновесия - узлов кристаллической решётки. Величина и направление смещения каждого из атомов относительно своего узла решётки меняются в процессе этих колебаний сложным образом, поскольку смещения всех атомов связаны между собой из-за наличия межатомных взаимодействий, т. е. являются коллективными. Однако периодичность кристаллической решётки и малая величина смещений позволяют достаточно просто описать именно коллективные движения атомов, что демонстрируют даже сильно упрощённые модели кристалла. В таких моделях предполагается, что смещения атомов могут происходить лишь в одном направлении; атомы представляются в виде частиц (шариков), расположенных в узлах кристаллической решётки и связанных между собой упругими пружинками, которые стремятся удерживать частицы в положениях равновесия.

При малых смещениях удерживающие силы можно считать пропорциональными смещениям, что называют гармоническим приближением, в котором уравнения движения частиц являются линейными и в классической механике  имеют  вид:

(1)

где n, n’ - радиус-векторы узлов кристаллической решётки, u(n) - смещение частицы относительно своего узла, m - масса частицы, α(n - n’) - жёсткости пружинок, соединяющих частицы, относящиеся к узлам с радиус-векторами n и n’ (величины α образуют матрицу упругих коэффициентов, или динамическую матрицу кристалла; смотри Модули упругости).

В гармоническом приближении любое движение атомов может быть представлено в виде суперпозиции нормальных колебаний (мод), которым отвечают независимые решения уравнений движения (1), имеющие вид бегущих (или стоячих) плоских волн типа

(2)

где u_s характеризует направление движения атома и зависит от типа атома (в реальном случае является вектором), k - так называемый квазиволновой вектор, направление которого определяет направление распространения бегущей волны (k = 2π/λ, где λ - длина волны, минимальное значение которой может быть выбрано равным или близким к наименьшему периоду кристаллической решётки а), ω_s - частота, t - время.

Нормальные колебания различаются квазиволновыми векторами, принимающими дискретные значения (в частности, точка k = 0 отвечает однородным смещениям), число которых равно числу элементарных ячеек в кристалле заданного объёма. В то же время каждому квазиволновому вектору отвечает 3v мод (v - число атомов в элементарной ячейке кристалла, множитель 3 отражает возможность каждого атома независимо смещаться в любом из трёх направлений в пространстве). Таким образом, число мод равно числу степеней свободы кристалла.

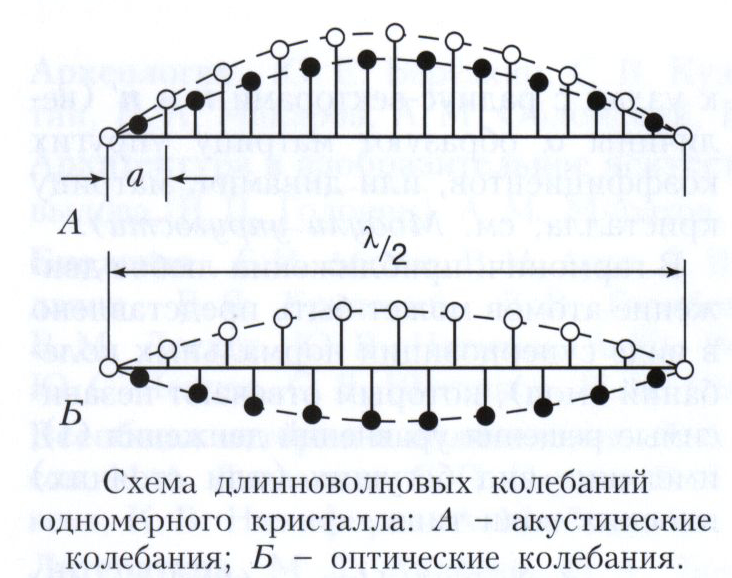
Для каждого s (s= 1, 2, ..., 3ν) существует своя (дисперсионная) зависимость ω_s (k), которая определяет соответствующую ветвь колебаний. В простой кристаллической решётке (v = 1) существуют только три ветви колебаний, которые называют акустическими. При малых волновых векторах (т. е. при λ много больших размеров элементарной ячейки a_i) каждая из них имеет линейный закон дисперсии (ω_s = c_sk, c_s порядка 10⁵ см·с^-1) для любого направления. Такие же колебания возникают при распространении звука в кристаллах. В сложной кристаллической решётке (ν > 1) существуют также и другие ветви колебаний, называемые оптическими; они имеют частоты порядка 10¹³ с^-1 при любых волновых векторах. В отличие от длинноволновых акустических колебаний, при  которых  все  атомы элементарной ячейки (и центр масс) движутся вместе (рис. А), оптические колебания характеризуются тем, что при λ >> а атомы движутся относительно центра масс элементарной ячейки, который сам не смещается (рис. Б). В ионных кристаллах элементарные ячейки содержат ионы противоположных знаков, и такие моды приводят к резонансному поглощению   световой   волны  в  ИК   области частот, в связи с чем они и названы оптическими.

Одной из важных характеристик спектра колебаний кристалла, которая используется при расчёте его свойств, является функция плотности состояний g(ω), которая равна числу нормальных мод на единицу интервала частот. При низких частотах она определяется распределением акустических мод и пропорциональна ω², а при некоторых высоких частотах (в частности, при максимальной частоте ω_макс) её производная по частоте обращается в бесконечность.

Интенсивность тепловых колебаний зависит от температуры кристалла. Для характеристики этой зависимости и оценки вклада колебаний кристалла в различные физические явления часто вводят Дебая температуру θ_D. При высоких температурах кристалла Т >> θ_D средняя энергия каждой моды равна kT (k - постоянная Больцмана), а средний квадрат смещения любого атома <u²> пропорционален температуре Т.

При низких температурах (Т << θ_D) такую энергию имеют только акустические длинноволновые моды, а энергии остальных мод ничтожно малы, что существенно уменьшает величину <u²>.

При квантовом описании динамики кристаллической решетки каждому нормальному колебанию с вектором k и частотой ω соответствует квазичастица с квазиимпульсом ħk (ħ - постоянная Планка) и энергией Е=kω. Эта квазичастица называется фононом и является элементарным возбуждением (квантом) в кристаллической решётке. Таким образом, колебания решётки рассматривают как газ фононов, что позволяет вычислять различные свойства кристалла методами статистической механики, развитыми для газов. В гармоническом приближении фононы не взаимодействуют друг с другом и, например, решёточная теплоёмкость вычисляется обычно как теплоёмкость идеального газа фононов при любых температурах. В металлах при высоких температурах рассеяние электронов на фононах даёт основной вклад в электрическое сопротивление.

В действительности колебания кристалла не являются гармоническими, что отражается введением в уравнение (1) нелинейных по смещениям слагаемых. Это приводит к тому, что нормальные колебания оказываются связанными друг с другом, а значит, фононы взаимодействуют между собой, т. е. образуют неидеальный газ. Такие взаимодействия являются причиной целого ряда эффектов. К ним относятся, например, тепловое расширение кристаллов, температурная зависимость частот нормальных мод, конечное время жизни фононов, теплопроводность. Одним из ярких проявлений динамической нелинейности являются фазовые переходы в кристаллах (например, сегнетоэлектриках) с так называемой мягкой модой. В таких кристаллах частота некоторого оптического фонона (мягкой моды) стремится к нулю при понижении температуры, что приводит к неустойчивости и перестройке структуры кристаллической решётки.

Существенное влияние на динамику кристаллической решётки могут оказывать различные дефекты, которые всегда существуют в реальных кристаллах (смотри Дефекты в кристаллах). Колебания кристаллов с дефектами уже нельзя представлять в виде совокупности плоских волн типа (2). Например, при замещении каких-либо атомов кристаллической решётки атомами другого типа (точечные дефекты) могут появляться локальные колебания, имеющие дискретные частоты, отличные от частот нормальных мод идеального кристалла (например, большие, чем ω_макс). Амплитуда таких колебаний резко убывает при удалении от дефекта. Вблизи дислокации (линейного дефекта) или плоского дефекта упаковки также могут появляться колебания, не проникающие в объём и отличающиеся законом дисперсии. К таким колебаниям относятся и звуковые колебания у свободной поверхности (волны Рэлея).

Лит.: Борн М., Хуан Кунь. Динамическая теория кристаллических решеток. М., 1958; Киттель Ч. Введение в физику твердого тела. М., 1978; Косевич А. М. Физическая механика реальных кристаллов. К., 1981.