Гистограмма

ГИСТОГРАММА (от греческого iστ?ς, здесь - столб, и ...грамма), один из видов графического представления экспериментальных данных. Обычно гистограмму строят следующим образом. Весь диапазон эмпирических значений X₁, ..., Х_n некоторой непрерывной случайной величины X разбивают на k интервалов (обычно равных) точками x₁, ..., x_k+1, где х₁ = min(X_1; ..., Х_n), x_k+1 = max(X₁, ..., Х_n), затем определяют абсолютные частоты m_i , i = 1, ..., k, равные числу наблюдений на интерва­лах [x_i, x_i+1), i= 1, …, k - 1, и [x_k , x_k+1], или относительные частоты h_i = m_i/n, i = 1, ..., k. На оси абсцисс отмечают точки x₁, ..., x_k+1 и строят прямоугольники, основаниями которых служат отрезки [х_i, x_i+1], i= 1, ..., k, равными m_i/(x_i+1 -x_i) или h_i/(x_i+1-х_i), так что площадь прямоугольника равна абсолютной либо относительной частоте. В случае равных длин интервалов высоты прямоугольников принимаются равными либо m_i , либо h_i. Выбор числа k интервалов разбиения зависит от неизвестного закона распределения случайной величины Х и объёма выборки. Универсальных рекомендаций по определению этого числа нет, чаще всего на практике используется формула Стерджеса k ≈ 1 + log₂n.

Пусть, например, измерение диаметра стволов 1000 елей дало результаты, указанные в таблице.

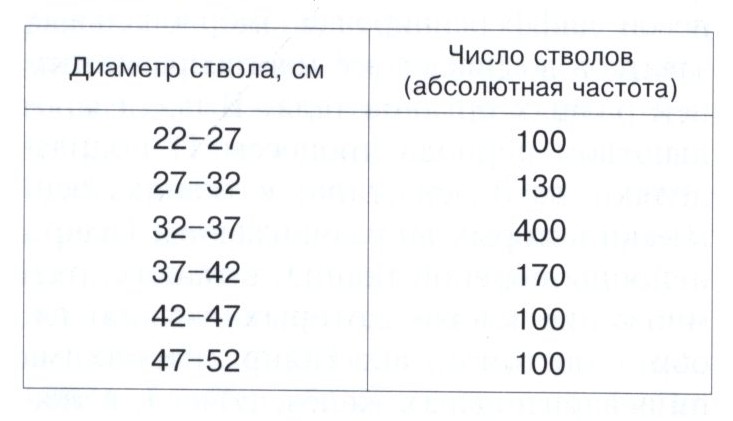
Гистограмма для этого примера с использованием абсолютных частот изображена на рисунке.

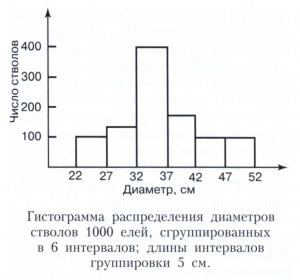
Аналогично можно строить гистограммы для дискретных и для векторных случайных величин. Построение гистограмм, в которых используются относительные частоты, является одним из методов непараметрического оценивания плотностей распределений непрерывных случайных величин, являющимся исторически первым и универсальным методом оценивания плотностей, однако его точность невысока.

Лит.: Смирнов Н.В. Теория вероятностей и математическая статистика. Избр. труды. М., 1970; Ченцов Н. Н. Статистические решающие правила и оптимальные выводы. М., 1972.