Гаусса принцип
ГАУССА ПРИНЦИП (принцип наименьшего принуждения), один из основных, наиболее общих дифференциальных вариационных принципов механики, выражающий экстремальные свойства действительного (истинного) движения механической системы по сравнению с другими движениями, кинематически возможными при тех же условиях. Предложен в 1829 году К. Гауссом, который ввёл функцию Z (принуждение):
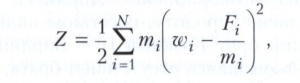
где N - число материальных точек системы, mi и wi - масса и ускорение i-той точки; Fi - равнодействующая активных сил, приложенных к i-той точке.
Гаусса принцип устанавливает, что в каждый момент времени истинное движение системы с идеальными связями, находящейся под действием активных сил, отличается от всех кинематически возможных движений, совершающихся из того же начального положения и с теми же начальными скоростями, тем свойством, что для истинного движения принуждение Z является минимальным. Математически это выражается равенством δΖ = 0, причём вариация берётся при неизменяемых координатах и скоростях точек системы, т. е. варьируются только ускорения.
Реклама
Используя уравнения движения точек системы miwi = Fi + Ri (где Ri - реакция связей), функцию Z можно представить в виде:
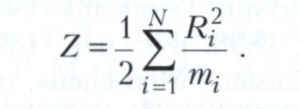
Условие, что величина Z минимальна для действительного движения, означает экстремальные свойства реакций связей: для действительного движения реакции связей минимальны.
Гаусса принцип эквивалентен Д’Аламбера-Лагранжа принципу и применим как к голономным, так и к неголономным системам. Из Гаусса принципа при выражении функции Z через независимые ускорения системы получаются дифференциальные уравнения движения системы в форме уравнений Аппеля. К Гаусса принципу тесно примыкает принцип прямейшего пути (Герца принцип).
Гаусса принцип обобщён на системы, частично освобождённые от связей, системы с неидеальными связями, а также на управляемые механические системы и сплошные среды. Гаусса принцип представляет собой физическую аналогию предложенному Гауссом наименьших квадратов методу, лежащему в основе многих статистических исследований.
В. М. Морозов.