Гиббса распределения

ГИББСА РАСПРЕДЕЛЕНИЯ, равновесные распределения вероятностей пребывания систем из большого числа частиц в состояниях, реализуемых в различных физических условиях. Гиббса распредления - фундаментальные законы статистической физики - установлены Дж. У. Гиббсом в 1901 и обобщены Дж. фон Нейманом в 1927 году для квантовой статистической механики.

Для получения Гиббса распредления вводится статистический ансамбль Гиббса: совокупность большого (в пределе бесконечно большого) числа копий данной системы в фиксированном макроскопическом состоянии, но в различных микросостояниях, которые характеризуются совокупностями координат q = (q₁, q₂, …, q_N) и импульсов р = (р₁, р₂, …, p_N) всех N частиц системы и соответствуют заданным макроскопическим условиям. Рассматривается распределение систем (членов ансамбля) в фазовом пространстве (р, q). Гиббса распредления в классической статистике зависят от координат и импульсов лишь через функцию Гамильтона Н(р, q) и не зависят от времени, удовлетворяя уравнению Лиувилля в стационарной форме.

Совокупность энергетически изолированных от окружающей среды систем с энергией ξ при постоянном объёме V с заданным числом частиц N (микроканонический ансамбль Гиббса) описывается микроканоническим распределением Гиббса f(р,q), согласно которому все состояния системы в узкой области энергий (Δ ξ << ξ) вблизи ξ равновероятны (основная гипотеза статистической механики).

Совокупность систем в контакте с термостатом (канонический ансамбль Гиббса), то есть систем с переменной энергией (фиксировано лишь её среднем значение) при заданных объёме V и числе частиц N и абсолютной температуре термостата Т, описывается каноническим распределением Гиббса:

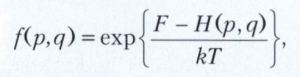
где Т - абсолютная температура, F - свободная энергия (Гельмгольца энергия), k - постоянная Больцмана.

Распределение вероятностей для систем в термическом и материальном контакте с термостатом и резервуаром частиц (большой канонический ансамбль Гиббса), т. е. для систем с переменными числом частиц N и энергией, определяемой функцией Гамильтона H_N, но с заданными температурой и химическим потенциалом μ, описывается большим каноническим распределением Гиббса:

где Ω- термодинамический потенциал в переменных V, μ, Т, определяемый из условия нормировки вероятности.

Совокупность систем в термическом и механическом контакте с окружающей средой (изобарически-изотермический ансамбль Гиббса), то есть с переменными энергией и объёмом, когда постоянным поддерживается давление Р с помощью, например, подвижного поршня, описывается изобарно-изотермическим распределением Гиббса:

где G - Гиббса энергия, т. е. термодинамический потенциал в переменных V, Р, Т.

Гиббса распределения в классической статистической механике являются предельными случаями Гиббса распределений квантовой статистической механики при таких плотностях и температурах, когда можно пренебречь квантовыми эффектами. Для квантовых систем Гиббса распределения имеют такую же форму, как и для классических, но в них вместо Н(р, q) входит энергия i-го квантового уровня системы.

Все Гиббса распределения  соответствуют максимуму информационной энтропии (смотри Энтропия) при различных дополнительных условиях: микроканоническим Гиббса распределениям  - при постоянном числе частиц и энергии; каноническим Гиббса распределениям  - при постоянном числе частиц и заданной средней энергии; большим каноническим Гиббса распределениям  - при заданных средней энергии и среднем числе частиц. Таким образом, все Гиббса распределения  являются наиболее вероятными распределениями, но при различных условиях.

Для вычисления термодинамических потенциалов все Гиббса распределения  эквивалентны, т. е. если с помощью одного из Гиббса распределений  вычислить соответствующий ему термодинамический потенциал, то затем при помощи термодинамических соотношений можно найти и все другие термодинамические потенциалы, соответствующие другим ансамблям.

Лит.: Зубарев Д. Н. Неравновесная статистическая термодинамика. М., 1971; Исихара А. Статистическая физика. М., 1973. Гл. 2, 3; Майер Дж., Гепперт-Майер М. Статистическая механика. 2-е изд. М., 1980. Гл. 3, 4; Гиббс Дж. Термодинамика. Статистическая механика. М., 1982; Ландау Л. Д., Лифшиц Е.М. Статистическая физика. 5-е изд. М., 2002. Ч. 1. Гл. 3.