Гильбертово пространство

ГИЛЬБЕРТОВО ПРОСТРАНСТВО, линейное бесконечномерное пространство, в котором задано скалярное произведение и выполнено условие полноты относительно нормы, порождаемой этим скалярным произведением. Названо по имени Д. Гильберта, который использовал эти пространства при решении уравнений математической физики. Гильбертово пространство представляет собой естественное обобщение конечномерного векторного (евклидова) пространства.

Обычно предполагается, что линейная структура Гильбертова пространства определена над полем комплексных чисел С, т. е. в Гильбертово пространство введено умножение элементов на комплексные числа, для каждой пары элементов введена их сумма и эти операции подчинены аксиомам векторного пространства. Если линейная структура определена над полем действительных чисел R, то говорят о действительном Гильбертовом пространстве. Скалярным произведением в Гильбертовом пространстве Н называется функция, которую обычно обозначают (х, у), со значениями в поле С (для действительного Гильбертово пространства - в поле R), определённая для произвольной пары элементов х, у Є Н и обладающая следующими свойствами:

(х, х)≥0, причём (х, х) = 0 тогда и только тогда, когда х = 0;

(х + у, z) = (х, z) + (у, z) для всех х, у, z Є Н;

(αх, у) = α(х, у) для всех α Є С и х, у Є Н;         

(х, у) = (у, х), где черта означает комплексное сопряжение.

В Гильбертово пространство можно ввести норму ||х|| элемента хЄН, положив ||x|| =√(х,х). При этом выполнены все свойства нормы: ||х|| > 0, ||αx|| = |α|·||x|| и ||х + y|| ≤ ||х|| +  ||у||. Для скалярного произведения и нормы справедливо неравенство Коши - Буняковского | (х, у) | ≤ || х || · || у ||.

Полнота Гильбертово пространства Н означает, что для любой последовательности элементов х₁, х₂,... Є Н, для которой ||х_k-х_n|| → 0 при k, n →∞, существует элемент х Є Н такой, что ||х_k-х|| → 0 при k→∞. Линейное бесконечномерное пространство со скалярным произведением, в котором условие полноты не выполнено, называют предгильбертовым. Если Н₀ - предгильбертово пространство, то существует единственное (с точностью до изоморфизма) Гильбертово пространство Н такое, что Н₀ с Н и Н₀ плотно в Н. Такое Гильбертово пространство Н называется пополнением пространства Н₀.

Всякое Гильбертово пространство является банаховым пространством. В Гильбертовом пространстве выполнено равенство параллелограмма

Наоборот, если в банаховом пространстве выполнено равенство параллелограмма, то это пространство можно рассматривать как Гильбертово пространство, поскольку в этом случае функция

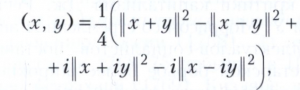
где i - мнимая единица, обладает всеми свойствами скалярного произведения (в случае действительного Гильбертова пространства последние два слагаемых опускаются).

Важными примерами Гильбертова пространства являются пространства l₂ и L₂(а, b). Пространство l₂ состоит из последовательностей комплексных чисел х = {x₁, х₂, ...}, удов­летворяющих условию ∑^∞_k=1| x_k|² < ∞.

Если х = {х₁, х₂, ...} и у = {у₁, у₂,...,} - две такие последовательности, то ряд ∑^∞_k=1 x_ky_k сходится и определяет скалярное произведение (х, у) в l₂. Пространство L₂(а, b) вводится как пополнение пространства непрерывных функций С[а, b] по норме, определяемой скалярным произведением (f, g) = ∫^b_a f(x)?g(x)dx.

Описание этого пополнения можно дать в терминах интеграла Лебега. Пространство L₂(а, b) состоит из измеримых по Лебегу функций f, для которых существует интеграл Лебега ∫^b_a |f(x)|²dx,  при этом функции отождествляются, если они отличаются лишь на множестве лебеговой меры нуль. Аналогично определяются Гильбертово пространство L₂(Ω), где Ω - область в n-мерном пространстве R_n.

Пространства l₂ и L₂(Ω) (как и большинство встречающихся в приложениях пространств) являются сепарабельными. Сепарабельность пространства означает, что в нём существует счётный набор элементов такой, что любой элемент пространства можно сколь угодно точно приблизить элементами из этого набора. В сепарабельном Гильбертовом пространстве Н существуют счётные ортонормированные базисы, то есть системы элементов {е_к}^∞_к=1, обладающие свойствами: ||е_k||=1, k =  1, 2, ..., (е_к, е_j) = 0 при k≠j, любой элемент х Є H представим в виде ряда x =∑^∞_k=1х_ке_к, где х_к - числа и ряд сходится по норме, т.е. ||х -∑ⁿ_k=1 x_ke_k||→ 0 при n → ∞. Такое представление однозначно, числа x_к равны (х, е_к) и называются коэффициентами Фурье элемента X по системе {е_к}^∞_k=1. Справедливо равенство ∑^∞_k=1| x_k|²= ||х||², называемое равенством Парсеваля; оно является бесконечномерным аналогом Пифагора теоремы. Примером ортонормированного базиса в l₂ является набор {е_n}^∞_n=1  где e_n - последовательность, n-я координата которой равна 1, а остальные координаты - нули. Примером ортонормированного базиса в L₂(0, 1) является система функций {√2 sin πnx}^∞_n=1. Все сепарабельные Гильбертовы пространства изоморфны друг другу.

В теории банаховых пространств вместе с пространствами В рассматриваются сопряжённые с ними пространства В*, состоящие из линейных непрерывных функционалов на В. Пространство, сопряжённое с Гильбертовым пространством Н, устроено просто, а именно: для каждого линейного непрерывного функционала f на Н существует элемент х* Є Н такой, что f(х) =  (х, х*) и ||f|| = ||х*||, то есть сопряжённое пространство Н* оказывается изоморфным исходному Гильбертову пространству Н. Этот факт делает Гильбертово пространство удобными для построения теории линейных операторов и даёт возможность ввести на Гильбертово пространство понятия самосопряжённого и унитарного операторов, играющих важную роль в функциональном анализе и математической физике.

Абстрактное определение Гильбертова пространства и основы общей теории линейных самосопряжённых и унитарных операторов были даны в работах Дж. фон Неймана, Ф. Рисса и американского математика М. Стоуна. Особую роль методы Гильбертова пространства стали играть после того, как в середине 1920-х годов были сформулированы основные принципы квантовой механики, согласно которым состояния квантово-механической системы интерпретируются как векторы Гильбертова пространства Н, а наблюдаемые (энергия, импульс и тому подобное) - как самосопряжённые операторы в Н. Важную роль в становлении теории операторов в Гильбертовом пространстве сыграли работы П. Л. Чебышева, А. А. Маркова (старшего) и Т. Стилтьеса по проблеме моментов, матрицам Якоби, теории ортогональных многочленов и непрерывным дробям.

Лит.: Морен К. Методы гильбертова пространства. М., 1965; Рисс Ф., Секефальви-Надь Б. Лекции по функциональному анализу. М., 1979; Гильберт Д. Избранные труды. М., 1998. Т. 2; Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. 7-е изд. М., 2004.