Грина формулы
ГРИНА ФОРМУЛЫ, формулы интегрального исчисления функций многих переменных, связывающие интегралы по области и по границе этой области. Простейшая Грина формула выражает двойной интеграл по области G через криволинейный интеграл по границе С области G и имеет вид
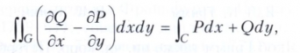
где функции Р и Q интегрируемы вместе со своими производными ∂Q/∂x, ∂P/∂y, ориентация на С задаётся обходом против часовой стрелки. Эта формула была известна ещё Л. Эйлеру (1771). Две следующие Грина формулы впервые опубликованы Дж. Грином в 1828 в связи с исследованиями по теории потенциала: при достаточно широких условиях на функции u и v
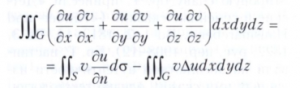
(так называемая первая или предварительная Грина формула) и
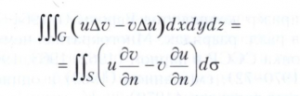
(так называемая вторая Грина формула). Здесь G - область трёхмерного пространства, поверхность S - граница этой области,
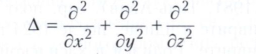
- оператор Лапласа, ∂u/∂n, ∂v/∂n - производные по направлению внешней нормали к S, dσ - элемент поверхности S, интеграл берётся по внешней стороне S. Смотри также Остроградского формула, Стокса формула.