Интегральное преобразование

ИНТЕГРАЛЬНОЕ ПРЕОБРАЗОВАНИЕ, функциональное преобразование вида

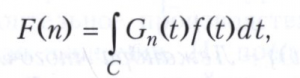
где С - конечный или бесконечный контур в комплексной плоскости, К(х, t) - ядро интегрального преобразования. Наиболее часто рассматриваются интегральные преобразования, для которых К(х, t)=К(xt) и С - действительная ось или её часть (а, b). Если - ∞ < а, b < ∞, то интегральное преобразование называется конечным. При К(х, t) = К(х - t) интегральное преобразование называется интегральным преобразованием типа свёртки. Если х и t - точки n-мерного пространства, а интегрирование ведётся по области этого пространства, то интегральное преобразование называется многомерным. Используются также дискретные интегральные преобразования вида

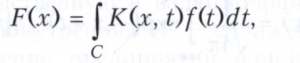
где n = 0, 1, 2,..., а {Gn(t)} - некоторая система функций, например Якоби многочлены. Формулы, позволяющие восстановить функцию f(t) по известной функции F(х), называются формулами обращения. Интегральные  преобразования определены также для обобщённых функций (распределений).

Интегральные  преобразования широко используются в математике и её приложениях, в частности при решении дифференциальных и интегральных уравнений математической физики. Наиболее важными для теории и приложений являются Фурье преобразование, Лапласа преобразование, преобразование Меллина.

Примерами интегрального преобразования являются преобразование Стилтьеса

где c_v(α, β) = J_ν(α) Y_v(ß) - Υ_ν(α)J_ν(β), J_v(x), Y_v(x) - цилиндрические функции 1-го и 2-го рода. Формула обращения для преобразования Вебера имеет вид

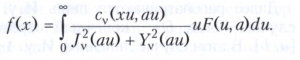
При а → 0 преобразование Вебера переходит в преобразование Ганкеля

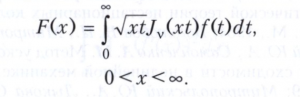
При v = ± 1/2 это преобразование сводится к синус и косинус-преобразованиям Фурье.

Примером преобразования свёртки является преобразование Вейерштрасса

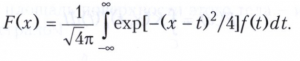
Преобразованием Бохнера называется преобразование

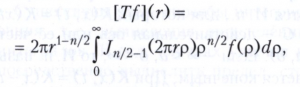
где J_v(х) - цилиндрическая функция 1-го рода порядка v, р - расстояние в Rⁿ. Преобразование

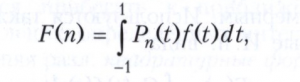
где {Pn(t)} - Лежандра многочлены, называется преобразованием Лежандра.

Ю. А. Брычков.