Инверсия в математике

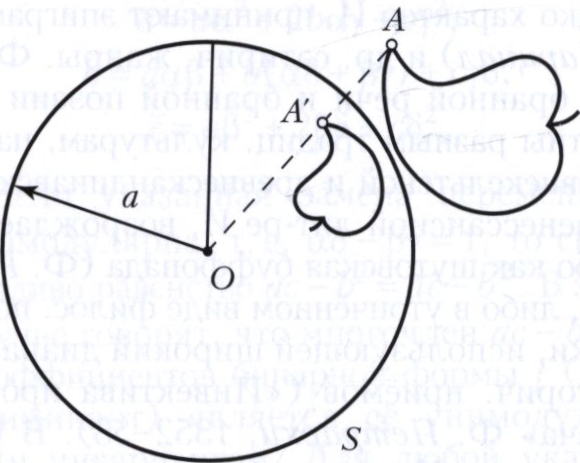ИНВЕРСИЯ в математике, преобразование плоскости, для которого некоторая точка О, называемая центром инверсии, фиксирована и любая точка А, не совпадающая с О, переходит в точку А’, лежащую на луче ОА, такую, что произведение длин отрезков ОА и ОА’ равно некоторому числу k, одному и тому же для любой точки А (рис.). Центр инверсии О иногда называют полюсом инверсии, а k - степенью или коэффициентом инверсии. Точки окружности S с центром О и радиусом √k переходят при инверсии сами в себя; образами внешних по отношению к S точек являются внутренние точки, а образами внутренних - внешние; центр инверсии не имеет образа. Иногда инверсия называется симметрией относительно окружности. Рассматривается также инверсия с k<0. Инверсия  с отрицательным коэффициентом k равносильна инверсии с тем же центром О и положительным коэффициентом |k|, сопровождаемой симметрией относительно точки О. Инверсия  с k > 0 называется гиперболической, а с k <0 - эллиптической инверсией или антиинверсией.

Прямая, проходящая через центр инверсии, преобразуется в себя. Прямая, не проходящая через центр инверсии, преобразуется в окружность без одной точки. Эта окружность проходит через точку О, и точка О исключается из окружности, обратное также верно. Окружности, ортогональные к окружности с центром О и радиусом √|k|, преобразуются сами в себя. В декартовых прямоугольных координатах инверсия с центром в начале координат может быть задана формулами

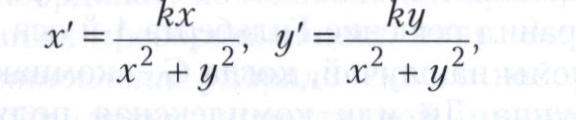
или, в плоскости комплексного переменного, формулой z’ = k/z̅, где черта означает комплексное сопряжение.

Аналогично определяется инверсия относительно сферы в пространстве.

Преобразование инверсии с 1824 года систематически применял швейцарский математик Я. Штейнер.