Изгиб

ИЗГИБ, вид деформации, характеризующийся искривлением (изменением кривизны) оси или срединной поверхности деформируемого тела под силовым, температурным или иным воздействием; при этом в поперечных сечениях деформируемого тела возникают изгибающие моменты. Если изгибающий момент в сечении является единственным внутренним силовым фактором, а поперечные и нормальная сила отсутствуют, изгиб называется чистым. Как правило, в поперечных сечениях бруса наряду с изгибающими моментами возникают также поперечные силы - такой изгиб называют поперечным. В инженерной практике рассматривают также изгиб продольный (характеризуется выпучиванием, то есть потерей устойчивости бруса под действием продольных сжимающих сил) и продольно-поперечный (вызывается одновременным действием сил, направленных вдоль и перпендикулярно оси бруса). Брус, работающий в основном на изгиб, называют балкой. Различают простой (плоский) и сложный изгиб. При простом изгибе все силы, в том числе и опорные реакции, лежат в одной из главных плоскостей бруса, то есть плоскостей, которые проходят через его ось и главные оси инерции поперечного сечения (смотри Момент инерции); изогнутая ось бруса в этом случае находится в этой же плоскости. Сложный изгиб вызывается силами, расположенными в разных плоскостях. При косом изгибе (частный случай сложного) плоскость действия суммарного изгибающего момента в сечении не совпадает ни с одной из главных осей инерции, направление прогибов (перемещений центра тяжести сечений в направлении главной оси) не совпадает с направлением действующей силы, а изогнутая ось бруса не лежит в плоскости действия сил (если нагрузка представляет собой плоскую систему сил).

Изгибающий момент в поперечном сечении определяется из уравнений равновесия отсечённой части конструкции (метод сечений). Для определения расчётных значений изгибающего момента строятся эпюры изгибающих моментов - графики, показывающие, как изменяется величина изгибающего момента по длине балки.

Расчёт балок на действие изгиба в упругой стадии производится в предположении справедливости гипотезы плоских сечений (поперечные сечения бруса, плоские до изгиба, остаются плоскими и после него) и гипотезы о ненадавливании продольных волокон (условно выделяемые нитевидные структурные слои бруса, т. е. волокна, параллельные его оси, при изгибе не давят друг на друга и не отрываются одно от другого).

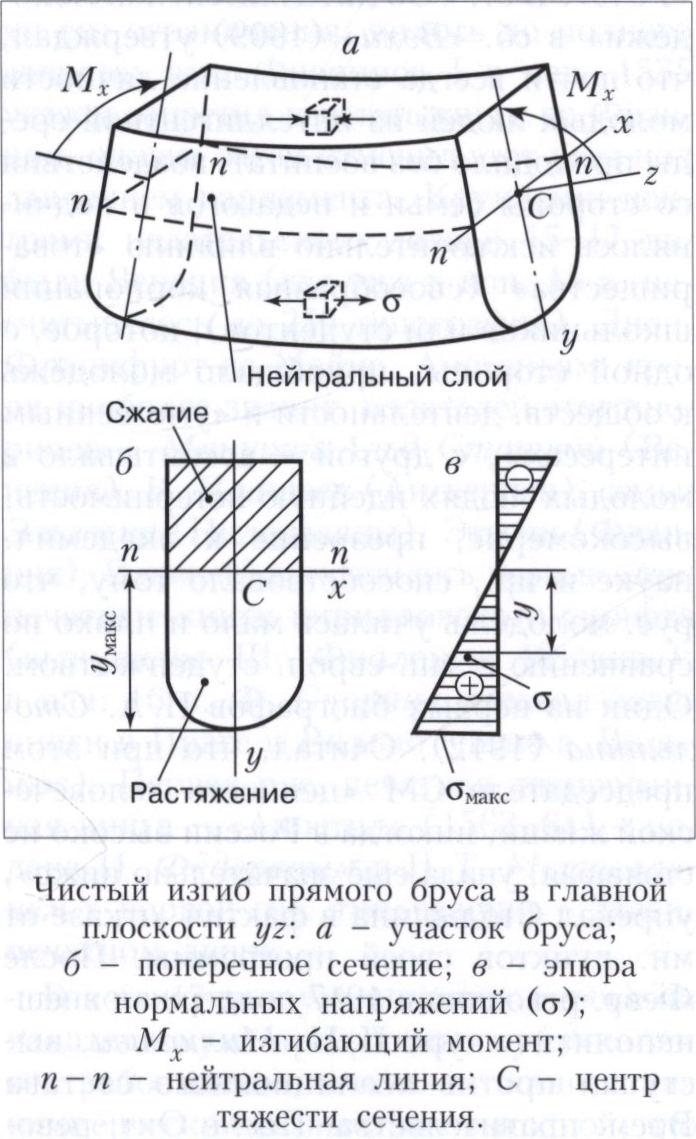
При плоском поперечном изгибе в поперечных сечениях возникают нормальные (σ) и касательные (τ) напряжения. В общем случае по высоте сечения имеются две зоны - растяжения (+) и сжатия (-), их разделяет нейтральный слой, удлинения в котором отсутствуют (σ = 0). Линия пересечения нейтрального слоя с плоскостью поперечного сечения называется нейтральной линией.

Нормальные напряжения в произвольном волокне, лежащем на расстоянии у от нейтральной линии (рис.), определяются по формуле σ =(M_x/M_y)·y, где М_х – изгибающий момент в сечении, I_X - момент инерции поперечного сечения относительно главной центральной оси.

Наибольшие нормальные напряжения возникают в точках, максимально удалённых от нейтральной линии:

σ_макс = ±M_x/W_x, где W_x = I_x/y_макс – момент сопротивления сечения. Касательные напряжения при поперечном изгибе определяются по формуле Журавского

где Q_y - поперечная сила в сечении, S_x - статический момент относительно оси х части площади поперечного сечения, расположенной выше уровня волокна, в котором определяются напряжения (выше уровня у), b_y - ширина сечения на уровне у.

Под влиянием изгиба ось бруса искривляется. Радиус кривизны ρ изгибаемого элемента зависит от величины изгибающего момента 1/ρ = M/EI_x, где EI_x – жесткость бруса при изгибе. В случае малых деформаций кривизна приближённо выражается второй производной от прогиба, поэтому дифференциальное уравнение оси изогнутого бруса имеет вид

Решением этого уравнения определяется упругая линия балки (форма её изогнутой оси).

Лит.: Сопротивление материалов. М., 1979; Федосьев В. И. Сопротивление материалов. М., 2007.