Канонические преобразования

КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ в классической механике, преобразования совокупности канонических переменных (q, р) к новым переменным (Q, Р), при которых канонические уравнения механики (смотри Гамильтона уравнения) сохраняют свою форму.

Канонические переменные q и р определяют состояние голономной механической системы, находящейся в поле потенциальных сил, в любой момент времени t и удовлетворяют уравнениям Гамильтона

(i = 1, ..., n),     (1)

где Н(t, q_i, p_i) - Гамильтона функция, n - число степеней свободы системы.

Невырожденные преобразования от переменных q и р к переменным Q и Р

Q = Q(q, р, t), Р = Р(q, р, t)  (2)

называются каноническими преобразованиями, если переменные Q_i и P_i также подчиняются уравнениям Гамильтона

(i = 1, ..., n), (3)

где Н’(t, Q_i, P_i) - некоторая новая функция Гамильтона. Предполагается, что соотношения (2) разрешимы относительно старых переменных

(i = 1, ..., n), (4)

Необходимым и достаточным условием каноничности преобразования (2) является существование функции S от старых (q, р) и новых (Q, Р) переменных и времени t, удовлетворяющей равенству

(5)

Функция S называется производящей функцией преобразования. Она может зависеть от всех 4n аргументов q_i, p_i, Q_i, P_i и времени t. Но поскольку имеются соотношения (2) и (4), достаточно считать её зависящей от 2n аргументов и времени, причём и аргументов должно быть старых и n - новых. В частности, если S = S (q, Q, t), то из условия (5) следует, что

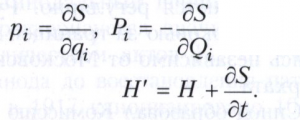
(i = 1, ..., n), (6)

Если функция S не зависит явно от времени, то Н’(Q, Р, t) = Н(q, р, t), где вместо q_i, p_i подставлены их выражения через переменные Q_i, P_i.

Канонические преобразования дают возможность заменить систему канонических уравнений движения (1) другой канонической системой (3) с функцией Гамильтона Н’(Q, Р, t), имеющей более простую структуру. Так, например, если найдено такое преобразование, что Н’ = 0, то решение канонических уравнений (3) Q_i(q, р, t) = const, P_i(q, р, t) = const (i = 1, ..., n), является совокупностью 2n независимых первых интегралов исходной канонической системы (1).

Можно показать, что в случае Н’= 0 из условий (5) и (6) следует уравнение для производящей функции  S (q, t)

(7)

которое называется Гамильтона-Якоби уравнением. Тем самым устанавливается связь между методом Гамильтона - Якоби интегрирования канонических уравнений при помощи нахождения полного интеграла уравнения в частных производных (7) и теорией канонических преобразований.

Якобиан канонических преобразований равен единице, откуда следует Лиувилля теорема об инвариантности фазового объёма в пространстве канонических переменных (q, р) относительно канонических преобразований (2).

Канонические преобразования удобно использовать в теории возмущений.

Лит.: Лурье А. И. Аналитическая механика. М., 1961.