Когерентное состояние
КОГЕРЕНТНОЕ СОСТОЯНИЕ, состояние квантовой системы, по своим свойствам максимально близкое к классическому состоянию. Для гармонического осциллятора в этом состоянии произведение дисперсий координаты σqq и импульса σрр принимает минимально возможное значение в рамках неопределенностей соотношения, то есть σqqσpp = h2/4, где h - постоянная Планка. При этом безразмерные дисперсии σqqσpp = h2/4, где h - постоянная Планка. При этом безразмерные дисперсии σqq/l2 и σpp/pl, где l2 = h/mω, p20 = hmω (m - масса, ω - частота осциллятора), равны 1/2, как для основного состояния классического осциллятора. Когерентное состояние осциллятора (с вектором состояния |а›) описывается волновой функцией, имеющей вид гауссова волнового пакета:
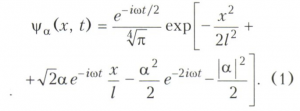
Здесь х - координата осциллятора, t - время, α = α1 + iα2 - комплексное число. Среднее значение координаты (х) осциллятора в когерентном состоянии при t = 0 выражается через действительную часть числа α, т. е. (х) = -√2α1, а среднее значение импульса (р) = √α2. Средние значения координаты и импульса с течением времени изменяются точно так же, как для классического осциллятора. Таким образом, когерентное состояние представляет собой нерасплывающийся со временем волновой пакет, центр которого движется по классической траектории, то есть совершает гармоническое колебание. Математическая характеристика когерентного состояния задаётся формулой
Реклама
![]()
где à - оператор уничтожения колебаний, который выражается через операторы координаты q̂ = х и импульса р̂ = -ihd/dx соотношением
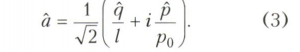
Существует и оператор рождения колебаний
![]()
Названия операторов связаны с тем, что действие а̂+ на состояние |n) гармонического осциллятора с заданной энергией Еn = hω(n+ 1/2), n= 0,1,2 переводит осциллятор в возбуждённое состояние |n + 1), увеличивая его энергию на квант hω, а действие оператора à на состояние |n) уменьшает энергию осциллятора на этот же квант.
Когерентное состояние квантовой системы можно представить в виде суммы n состояний осциллятора с заданными уровнями энергии En = hω(n + 1/2), n = 0,1,2 то есть
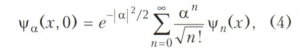
где ψn(х) выражается через полином Эрмита.
Электромагнитное поле является набором мод гармонии, колебаний осцилляторов поля (фотонов). Поэтому когерентное состояние квантованного электромагнитного поля максимально близко соответствует колебаниям классического электромагнитного поля, обладая при этом свойством когерентности. Для фотонов в когерентном состоянии |а) формуле разложения волновой функции осциллятора (4) соответствует формула разложения когерентного состояния:
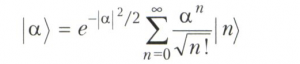
по состояниям |n) с заданным числом фотонов.
Когерентные состояния используются для описания не только осциллятора в квантовой механике и фотонов в квантовой электродинамике, но и квантовых состояний любых бозонов, операторы рождения а̂+ и уничтожения а̂ которых удовлетворяют коммутационным соотношениям [а̂, а̂+] = 1. Такими бозонными полями являются, например, пионы и все элементарные частицы с целым спином, а также кванты звука - фононы. Свойства сверхтекучести и сверхпроводимости также можно объяснить тем, что в когерентном состоянии находятся сверхтекучая компонента в жидком гелии и куперовские пары в сверхпроводниках (смотри Квантовая когерентность).
Лит.: Когерентные состояния в квантовой теории. М., 1972; Малкин И. А., Манько В. И. Динамические симметрии и когерентное состояние квантовых систем. М., 1979.
В. И. Манько.