Когерентность
КОГЕРЕНТНОСТЬ (от латинского cohaerens - находящийся в связи), коррелированность (согласованность) колебаний или волн, в том числе случайных, протекающих в различных точках и в различные моменты времени, позволяющая наблюдать при их сложении интерференционную картину. Колебания полностью когерентны при постоянной разности фаз между ними. При разности фаз, флуктуирующей в пределах 2π за время наблюдения, колебания можно считать некогерентными.
Понятие «когерентность» применялось сначала к волнам оптического диапазона (смотри Когерентность света), однако когерентность характерна для волн любой природы, для которых выполняется суперпозиции принцип (электромагнитных волн любого диапазона, волн вероятности в квантовой механике, упругих волн, волн в плазме и др.).
Пространственно-временное изменение поля обычно измеряется как усреднённый по времени сигнал с квадратичного детектора, а степень связанности (согласованности) полей в различных пространственно-временных точках количественно характеризуется корреляционными функциями различных порядков (обычно чётных). Вид корреляционных функций зависит от природы волн. Скалярные волны с напряжённостью поля Е(r, t) = Re[u(r, t)], где u(r, t) - комплексная амплитуда, характеризуются скалярными корреляционными функциями порядка 2n:
Реклама
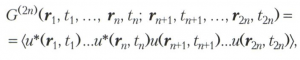
где rk, tk - пространственно-временные координаты (k = 1,22n), звёздочка означает комплексное сопряжение. Для векторных полей корреляционная функция является тензором второго ранга. Угловые скобки означают усреднение по ансамблю реализаций случайного процесса u(r, t). В расчётах обычно используют двухточечную функцию взаимной корреляции G(2)(r1, t1, r2, t2), среднюю интенсивность волны I(r,t) = G(2)(r,t;r,t), корреляционную функцию интенсивностей G(4)(r1, t1 , r2, t2; r1,t1, r2,t2). Наиболее просто вычисляются корреляционные функции поля для источников, имеющих малую угловую расходимость и состоящих из независимых элементарных излучателей.
Если полное волновое поле образовано суммой полей от двух источников: u(r, t) = u(r1, t1) + u(r2, t2), где связь между точками (r, t), (r1, t1) и (r2, t2) определяется геометрией эксперимента, то сигнал с квадратичного детектора в точке наблюдения (r, t) равен:
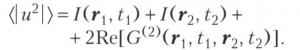
Для количественного определения когерентности полей в пространственно-временньк точках (r1, t1) и (r2, t2) вводится величина
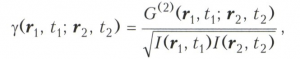
называемая степенью взаимной когерентности. Согласно определению, |γ (r1, t1;r2,t2)| ≤ 1. При (r1, t1) = (r2, t2) величина |γ | = 1. При условии l(r1, t1) = l(r2,t2) относительный контраст интерференционной картины
![]()
совпадает с |γ |. Характерный масштаб τ0 спадания функции |γ(r, t;r, t + τ)| по τ = t2 - t1 есть время когерентности, а величина сτ0 - длина когерентности (с - скорость света).
Смещение волнового пучка с узким угловым спектром, близкого к плоской волне, в поперечном направлении приводит к уменьшению степени когерентности. Характерный масштаб r0 уменьшения степени когерентности называется поперечным радиусом когерентности. При распространении волны от протяжённого источника, образованного совокупностью независимых излучателей, поперечный радиус когерентности увеличивается с увеличением расстояния от источника. Величина (r0)2сτ0 есть объём когерентности; в его пределах случайная фаза поля меняется менее чем на π и колебания частично когерентны.
Понятие «когерентности», основанное на сохранении фазовых соотношений между квантово-механическими амплитудами вероятности, наряду с понятием интерференции состояний широко используется также в квантовой механике, квантовой оптике. В этом случае корреляционные функции строятся таким же образом, однако и* заменяют на оператор рождения фотона Е+, u - на оператор уничтожения фотона Е, а сама корреляционная функция становится оператором, который действует на вектор состояния поля.
При описании динамики резонансных переходов в атомах или молекулах под действием коротких световых импульсов длительностью менее характерного времени релаксации населённостей уровней также учитывается когерентность взаимодействия. При этом можно наблюдать когерентные процессы - оптические нутации, затухание свободной поляризации, оптическое эхо, самоиндуцированную прозрачность (смотри Нелинейная оптика).
Создание лазеров, генерирующих сверхкороткие световые импульсы (длительностью единицы - сотни фемтосекунд), позволило получать широкополосные поля с высокой степенью когерентности, которые описываются корреляционными функциями высших порядков.
Лит.: Клаудер Дж., Сударшан Э. Основы квантовой оптики. М., 1970; Перина Я. Когерентность света. М., 1974; Ландау Л. Д., Лифшиц Е. М. Теория поля. 8-е изд. М., 2003.
Л. А. Мельников.