Конечных приращений формула

КОНЕЧНЫХ ПРИРАЩЕНИЙ ФОРМУЛА (формула Лагранжа), одна из основных формул дифференциального исчисления, связывающая приращение функции f(х) на отрезке [а, b] со значениями её производной

f(b) - f(а) = f ‘(ξ)(b - а),

где ξ - некоторая точка, удовлетворяющая условию а < ξ < b. Конечных приращений формула справедлива, если функция f(х) непрерывна на отрезке [а, b] и имеет производную в каждой точке интервала (а, b). Геометрически конечных приращений формула означает, что на графике функции у = f(х) существует точка (ξ,f(ξ)), в которой касательная параллельна прямой, соединяющей точки ia, f(а)) и (b, f(b)). Конечных  приращений формулу часто записывают в виде

f(х + h) - f(х) = f ‘(х + θh)h,

где h - приращение аргумента, θ - некоторое число, удовлетворяющее неравенствам 0 < θ < 1.

Конечных  приращений формула установлена Ж. Лагранжем (1797), она является простейшим случаем Тейлора формулы с остаточным членом в форме Лагранжа.

Имеются многочисленные разнообразные обобщения конечных приращений формулы. Например, справедливы формула Коши о приращениях двух функций

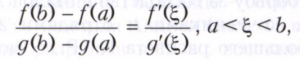
и формула для приращений функции многих переменных

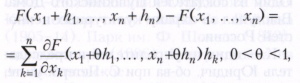
где h₁, ... , h_n - приращения аргументов, ∂F/∂х_к - частная производная функции F по переменной x_k, k=1,... , n.